Polynomial Roots

A root of a polynomial 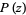 is a number  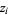such that 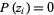. The fundamental theorem of algebra states that a polynomial  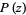of degree  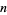has 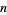 roots, some of which may be degenerate. For example, the roots of the polynomial

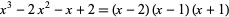(1)

are 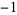, 1, and 2. Finding roots of a polynomial is therefore equivalent to polynomial factorization into factors of degree 1.

Any polynomial can be numerically factored, although different algorithms have different strengths and weaknesses.

The roots of a polynomial equation may be found exactly in the Wolfram Language using Roots[lhs==rhs, var], or numerically using NRoots[lhs==rhs, var]. In general, a given root of a polynomial 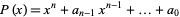 is represented as Root[#^n+a[n-1]#^(n-1)+...+a[0]&, k], where 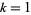, 2, ...,  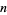is an index identifying the particular root and the pure function polynomial is irreducible. Note that in the Wolfram Language, the ordering of roots is different in each of the commands Roots, NRoots, and Table[Root[p, k], k, n].

In the Wolfram Language, algebraic expressions involving Root objects can be combined into a new Root object using the command RootReduce.

In this work, the 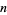th root of a polynomial  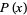in the ordering of the Wolfram Language's Root object is denoted 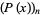, where  is a dummy variable. In this ordering, real roots come before complex ones and complex conjugatepairs of roots are adjacent. For example,

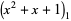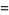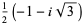			(2)
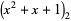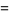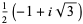			(3)

and

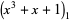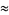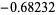			(4)
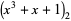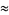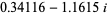			(5)
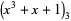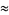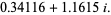			(6)

Let the roots of the polynomial

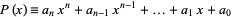(7)

be denoted 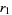, , 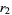..., 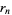. Then Vieta's formulas give

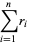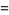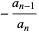			(8)
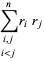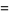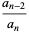			(9)
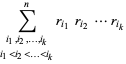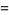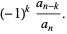			(10)

These can be derived by writing

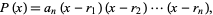(11)

expanding, and then comparing the coefficients with (◇).

Given an 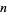th degree polynomial 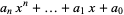, the roots can be found by finding the eigenvalues  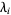of the matrix

(12)

and taking 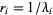. This method can be computationally expensive, but is fairly robust at finding close and multiple roots.

If the coefficients of the polynomial

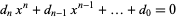(13)

are specified to be integers, then rational roots must have a numerator which is a factor of 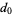 and a denominatorwhich is a factor of  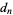(with either sign possible). This is known as the polynomial remainder theorem.

If there are no negative roots of a polynomial (as can be determined by Descartes' sign rule), then the greatest lower bound is 0. Otherwise, write out the coefficients, let 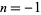, and compute the next line. Now, if any coefficients are 0, set them to minus the sign of the next higher coefficient, starting with the second highest order coefficient. If all the signs alternate,  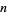is the greatest lower bound. If not, then subtract 1 from 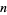, and compute another line. For example, consider the polynomial

(14)

Performing the above algorithm then gives

0	2	2		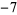1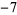
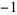	2	0		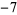8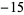
--	2		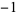	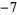8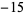
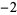	2		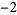	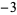7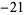
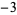	2		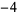5		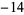35

so the greatest lower bound is .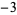

If there are no positive roots of a polynomial (as can be determined by Descartes' sign rule), the least upper bound is 0. Otherwise, write out the coefficients of the polynomials, including zeros as necessary. Let 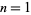. On the line below, write the highest order coefficient. Starting with the second-highest coefficient, add  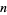times the number just written to the original second coefficient, and write it below the second coefficient. Continue through order zero. If all the coefficients are nonnegative, the least upper bound is 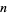. If not, add one to  and repeat the process again. For example, take the polynomial

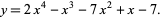(15)

Performing the above algorithm gives

0	2		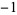	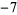1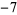
1	2	1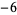
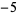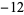2	2	3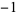
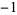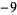3	2	5	8	25	68

so the least upper bound is 3.

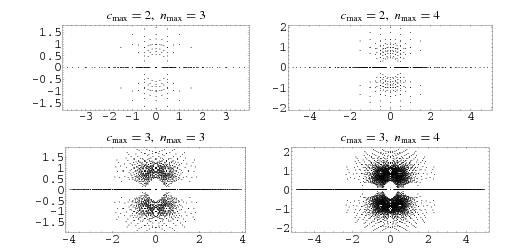
Plotting the roots in the complex plane of all polynomials up to some degree with integer coefficients less than some cutoff integer in absolute value shows the beautiful structure illustrated above (Trott 2004, p. 23).

An even more stunning figure is obtained by plotting all roots of all polynomials with coefficients 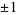 up to degree 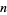(Borwein and Jörgenson 2001; Pickover 2002; Bailey et al. 2007, p. 18).

REFERENCES:

Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action.Wellesley, MA: A K Peters, 2007.

Bharucha-Reid, A. T. and Sambandham, M. Random Polynomials. New York: Academic Press, 1986.

Borwein, P. and Jörgenson, L. "Visible Structures in Number Theory." Amer. Math. Monthly 108, 897-911, 2001.

Borwein, P. Computational Excursions in Analysis and Number Theory. New York: Springer-Verlag, 2002.

Odlyzko, A. M.; and Poonen, B. "Zeros of Polynomials with 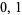 Coefficients." L'Enseignement Math. 39, 317-348, 1993.

Pan, V. Y. "Solving a Polynomial Equation: Some History and Recent Progress." SIAM Rev. 39, 187-220, 1997.

Pickover, C. A. The Mathematics of Oz: Mental Gymnastics from Beyond the Edge. New York: Cambridge University Press, pp. 286-287, 2002.

Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.