Complex Conjugate

The complex conjugate of a complex number 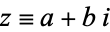 is defined to be

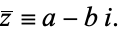(1)

The conjugate matrix of a matrix 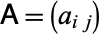 is the matrix obtained by replacing each element  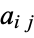with its complex conjugate,  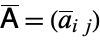(Arfken 1985, p. 210).

The complex conjugate is implemented in the Wolfram Language as Conjugate[z].

Note that there are several notations in common use for the complex conjugate. Applied physics and engineering texts tend to prefer 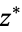, while most modern math and theoretical physics texts favor 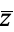. Unfortunately, the notation  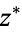is also commonly used to denote adjoint operators matrices. Because of these mutually contradictory conventions, care is needed when consulting the literature. In this work,  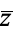is used to denote the complex conjugate.

Common notational conventions for complex conjugate are summarized in the table below.

notation	references
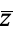	This work; Abramowitz and Stegun (1972, p. 16), Anton (2000, p. 528), Harris and Stocker (1998, p. 21), Golub and Van Loan (1996, p. 15), Kaplan (1981, p. 28), Kaplan (1992, p. 572), Krantz (1999, p. 2), Kreyszig (1988, p. 568), Roman (1987, p. 534), Strang (1988, p. 220), Strang (1993)
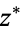	Arfken (1985, p. 356), Bekefi and Barrett (1987, p. 616), Press et al. (1989, p. 397), Harris and Stocker (1998, p. 21), Hecht (1998, p. 18), Herkommer (1999, p. 262)

In linear algebra, it is common to apply both the complex conjugate and transpose to the same matrix. The matrix obtained from a given matrix 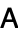 by this combined operation is commonly called the conjugate transpose  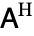of 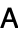. However, the terms adjoint matrix, adjugate matrix, Hermitian conjugate, and Hermitian adjoint are also used, as are the notations  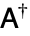and 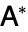. In this work,  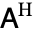is used to denote the conjugate transpose matrix and  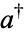is used to denote the adjoint operator.

By definition, the complex conjugate satisfies

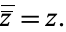(2)

The complex conjugate is distributive under complex addition,

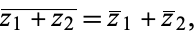(3)

since

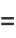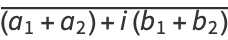			(4)
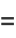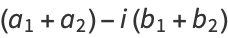			(5)
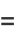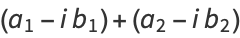			(6)
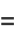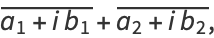			(7)

and distributive over complex multiplication,

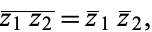(8)

since

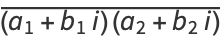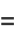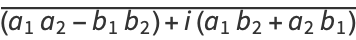			(9)
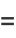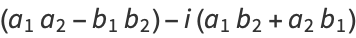			(10)
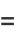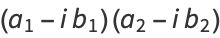			(11)
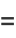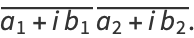			(12)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 16, 1972.

Anton, H. Elementary Linear Algebra, 8th ed. New York: Wiley, 2000.

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 355-356, 1985.

Bekefi, G. and Barrett, A. H. Electromagnetic Vibrations, Waves, and Radiation. Cambridge, MA: MIT Press, p. 616, 1987.

Golub, G. and Van Loan, C. Matrix Computations, 3rd ed. Baltimore, MD: Johns Hopkins University Press, 1996.

Hecht, E. Optics, 3rd ed. Reading, MA: Addison-Wesley, p. 18, 1998.

Herkommer, M. A. Number Theory: A Programmer's Guide. New York: McGraw-Hill, p. 262, 1999.

Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science. New York: Springer-Verlag, p. 21, 1998.

Kaplan, W. Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley, 1992.

Kaplan, W. Advanced Mathematics for Engineers. Reading, MA: Addison-Wesley, 1981.

Krantz, S. G. "Complex Conjugate." §1.1.3 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 2, 1999.

Kreyszig, E. Advanced Engineering Mathematics, 6th ed. New York: Wiley, p. 568, 1988.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, 1989.

Roman, S. "The Conjugate of a Complex Number and Complex Division." §11.2 in College Algebra and Trigonometry. San Diego, CA: Harcourt, Brace, Jovanovich, pp. 534-541, 1987.

Strang, G. Introduction to Linear Algebra. Wellesley, MA: Wellesley-Cambridge Press, 1993.

Strang, G. Linear Algebra and its Applications, 3rd ed. Philadelphia, PA: Saunders, 1988.