المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Caudrey-Dodd-Gibbon-Sawada-Kotera Equation |
 1016
 02:15 مساءً
date: 13-7-2018 |
Author : Aiyer, R. N.; Fuchssteiner, B.; and Oevel, W 
Book or Source : "Solitons and Discrete Eigenfunctions of the Recursion Operator of Non-Linear Evolution Equations: I. The Caudrey-Dodd-Gibbon-Sawada-Kotera... 
Page and Part : ...|
Read More
Date: 18-7-2018
1100
Date: 21-7-2018
913
Date: 23-7-2018
965
|
The partial differential equation
 |
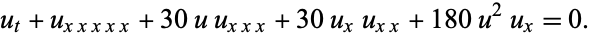REFERENCES:
Aiyer, R. N.; Fuchssteiner, B.; and Oevel, W. "Solitons and Discrete Eigenfunctions of the Recursion Operator of Non-Linear Evolution Equations: I. The Caudrey-Dodd-Gibbon-Sawada-Kotera Equations." J. Phys. A: Math. Gen. 19, 3755-3770, 1986.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 132, 1997.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
