


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-7-2018
Date: 11-6-2018
Date: 26-12-2018
|
The Legendre differential equation is the second-order ordinary differential equation
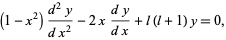 |
(1) |
which can be rewritten
![d/(dx)[(1-x^2)(dy)/(dx)]+l(l+1)y=0.](http://mathworld.wolfram.com/images/equations/LegendreDifferentialEquation/NumberedEquation2.gif) |
(2) |
The above form is a special case of the so-called "associated Legendre differential equation" corresponding to the case 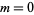 . The Legendre differential equation has regular singular points at
. The Legendre differential equation has regular singular points at 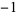 , 1, and
, 1, and 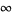 .
.
If the variable  is replaced by
is replaced by 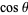 , then the Legendre differential equation becomes
, then the Legendre differential equation becomes
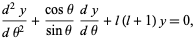 |
(3) |
derived below for the associated (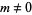 ) case.
) case.
Since the Legendre differential equation is a second-order ordinary differential equation, it has two linearly independent solutions. A solution 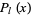 which is regular at finite points is called a Legendre function of the first kind, while a solution
which is regular at finite points is called a Legendre function of the first kind, while a solution 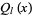 which is singular at
which is singular at 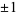 is called a Legendre function of the second kind. If
is called a Legendre function of the second kind. If 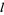 is an integer, the function of the first kind reduces to a polynomial known as the Legendre polynomial.
is an integer, the function of the first kind reduces to a polynomial known as the Legendre polynomial.
The Legendre differential equation can be solved using the Frobenius method by making a series expansion with 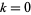 ,
,
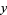 |
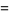 |
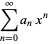 |
(4) |
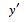 |
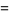 |
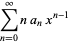 |
(5) |
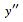 |
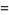 |
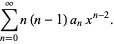 |
(6) |
Plugging in,
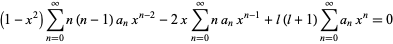 |
(7) |
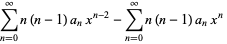 |
(8) |
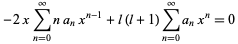 |
(9) |
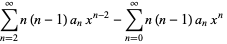 |
(10) |
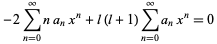 |
(11) |
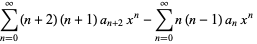 |
(12) |
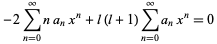 |
(13) |
![sum_(n=0)^infty{(n+1)(n+2)a_(n+2)+[-n(n-1)-2n+l(l+1)]a_n}=0,](http://mathworld.wolfram.com/images/equations/LegendreDifferentialEquation/NumberedEquation5.gif) |
(14) |
so each term must vanish and
![(n+1)(n+2)a_(n+2)+[-n(n+1)+l(l+1)]a_n=0](http://mathworld.wolfram.com/images/equations/LegendreDifferentialEquation/NumberedEquation6.gif) |
(15) |
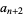 |
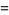 |
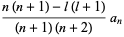 |
(16) |
 |
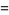 |
)/((n+1)(n+2))a_n.](http://mathworld.wolfram.com/images/equations/LegendreDifferentialEquation/Inline32.gif) |
(17) |
Therefore,
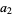 |
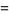 |
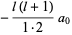 |
(18) |
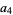 |
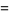 |
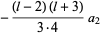 |
(19) |
 |
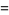 |
![(-1)^2([(l-2)l][(l+1)(l+3)])/(1·2·3·4)a_0](http://mathworld.wolfram.com/images/equations/LegendreDifferentialEquation/Inline41.gif) |
(20) |
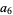 |
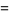 |
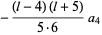 |
(21) |
 |
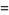 |
![(-1)^3([(l-4)(l-2)l][(l+1)(l+3)(l+5)])/(1·2·3·4·5·6)a_0,](http://mathworld.wolfram.com/images/equations/LegendreDifferentialEquation/Inline47.gif) |
(22) |
so the even solution is
![y_1(x)=1+sum_(n=1)^infty(-1)^n([(l-2n+2)...(l-2)l][(l+1)(l+3)...(l+2n-1)])/((2n)!)x^(2n).](http://mathworld.wolfram.com/images/equations/LegendreDifferentialEquation/NumberedEquation7.gif) |
(23) |
Similarly, the odd solution is
![y_2(x)=x+sum_(n=1)^infty(-1)^n([(l-2n+1)...(l-3)(l-1)][(l+2)(l+4)...(l+2n)])/((2n+1)!)x^(2n+1).](http://mathworld.wolfram.com/images/equations/LegendreDifferentialEquation/NumberedEquation8.gif) |
(24) |
If 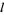 is an even integer, the series
is an even integer, the series 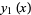 reduces to a polynomial of degree
reduces to a polynomial of degree  with only even powers of
with only even powers of  and the series
and the series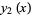 diverges. If
diverges. If  is an odd integer, the series
is an odd integer, the series 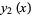 reduces to a polynomial of degree
reduces to a polynomial of degree 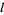 with only odd powers of
with only odd powers of  and the series
and the series 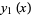 diverges. The general solution for an integer
diverges. The general solution for an integer 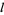 is then given by the Legendre polynomials
is then given by the Legendre polynomials
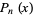 |
 |
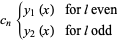 |
(25) |
 |
 |
 |
(26) |
where 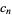 is chosen so as to yield the normalization
is chosen so as to yield the normalization 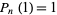 and
and 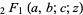 is a hypergeometric function.
is a hypergeometric function.
A generalization of the Legendre differential equation is known as the associated Legendre differential equation.
Moon and Spencer (1961, p. 155) call the differential equation
 |
(27) |
the Legendre wave function equation (Zwillinger 1997, p. 124).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 332, 1972.
Moon, P. and Spencer, D. E. Field Theory for Engineers. New York: Van Nostrand, 1961.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, 1997.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|