


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-7-2018
Date: 22-5-2018
Date: 30-5-2018
|
The Burridge-Knopoff model is a system of differential equations used to model earthquakes using 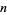 points on a straight line, each of mass
points on a straight line, each of mass 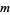 , that interact with each other via springs, and in which all masses are subject to a force that is proportional to the distances
, that interact with each other via springs, and in which all masses are subject to a force that is proportional to the distances 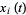 of the masses from their equilibrium position and to a friction force
of the masses from their equilibrium position and to a friction force 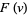 , where
, where 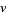 is the velocity,
is the velocity,

REFERENCES:
Burridge, R. and Knopoff, L. Bull. Seis. Soc. Amer. 57, 341, 1967.
de Sousa Vieira, M. Phys. Rev. Lett. 82, 201, 1999.
de Sousa Vieira, M. "A Simple Deterministic Self-Organized Critical System." 23 Jan 2000. http://arxiv.org/abs/cond-mat/9907201.
Ferguson, C. D.; Klein, W.; and Rundle., J. B. Computers Physics 12, 34 1998.
Hähner, P. and Drossinos, Y. Physica A 260, 391, 1998.
Muratov, C. B. "Traveling Wave Solutions in the Burridge-Knopoff Model." 14 Jan 1999. http://arxiv.org/abs/patt-sol/9901003.
Place, D. and Villedieu, P. J. Comput. Phys. 150, 332,1999.
Webman, I.; Gruver, J. L.; and Havlin, S. "Sliding Objects with Random Friction." 12 Apr 1999. http://arxiv.org/abs/cond-mat/9904148.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, pp. 12-13, 2004. http://www.mathematicaguidebooks.org/.
Xu, H.-J and Knopoff, L. Phys. Rev. E 50, 3577, 1994.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|