A set of operations is functionally complete provided every propositional function can be expressed entirely in terms of operations in the set. To exhibit a functionally complete set, we recall that every propositional function has a truth table.  Further, every truth table corresponds to a unique expression in dis- junctive (or conjunctive) normal form, involving only the operations  (+),(.) and ('). Hence the set {+,. , '} is functionally complete.

Since the proposition pq is equal to the proposition (p' + q')' by the law of De Morgan, it is possible to replace each occurrence of conjunction in any propositional function with an equivalent expression involving only (+) and ('). This shows that {+, '} is a functionally complete set of operations. Other functionally complete sets are {.,΄}and { →, '}.

It is possible to define a single operation which constitutes a functionally complete set. Suppose that we define p↓q by Table 1-1. This

TABLE 1-1

DEFINITION OF p↓q

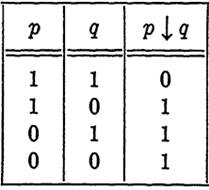
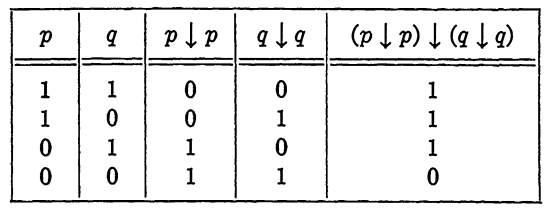
operation can be interpreted as "not both p and q." To see how this operation alone constitutes a functionally complete set, consider Table 1-2. From this table, we observe that p' = p ↓ p and p + q = (p↓p) I (q ↓q). But we have shown that every propositional function can be expressed in terms of (+) and ('). Each occurrence of (+) and (')  may be replaced by the equivalent expression in terms of (↓), and henceevery propositional function can be written entirely in terms of the operation (↓). The operation (↓) is one of two operations known as Shefer stroke functions.

Table 1-2

مواضيع ذات صلة

Zero Polynomial

Kronecker,s Polynomial Theorem

THE ALGEBRA OF SETS-The number of elements in a set

THE ALGEBRA OF SETS-Solution of equations

THE ALGEBRA OF SETS-Conditional equations

THE ALGEBRA OF SETS-Properties of set inclusion

THE ALGEBRA OF SETS- Expanding, factoring, and simplifying

THE ALGEBRA OF SETS-Fundamental laws

THE ALGEBRA OF SETS-Venn diagrams

THE ALGEBRA OF SETS-The combination of sets

THE ALGEBRA OF SETS-Element and set

THE ALGEBRA OF SETS-Introduction