مركز الكتلة

عند حساب GPE للأجسام الحقيقية لابد أن ان نتساءل من أي نقطة يقاس ارتفاع الجسم عن مستو الإسناد؟ إذا رفع الجسم بحيث لا يعاني أي دوران ، فإن كل نقط الجسم سوف ترتبع بنفس المقدار ، ومن ثم يمكن استخدام أي نقطة لقياس GPE. ولكن لنفرض مثلاً أننا نعالج حالة قالب مستطيل منتظم مستقر على وجهه الأكبر كما هو مبين بالشكل 1)). ما مقدار الشغل اللازم بذله لكي يقلب هذا القالب على أصغر وجه له؟

الشكل 1))

أن هذا الشغل يساوي الزيادة في GPE لأن الأنواع الأخرى من طاقة القالب لا تتغير:

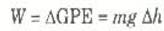
لاحظ مع ذلك أن ارتفاعات جميع نقط القالب لا تتغير بنفس المقدار. وحيث أن مختلف أجزاء القالب تتغير ارتفاعاتها الرأسية بمقادير مختلفة لن يمكننا تحديد قيمة hΔ بشكل حاسم .

إن مفتاح الحل لمعرفة قيمة hΔ الواجب استخدامها في المعادلة السابقة هو ما يسمى مركز كتلة (c. m.) الجسم. فإذا كانت عجلة الجاذبية عند مختلف نقط الجسم ثابتة فإن مركز الثقل ينطبق على مركز الكتلة. أن مركز ثقل c.m. الأجسام المتماثلة هندسياً والمنتظمة الكثافة يقع في مراكزها الهندسية، وبناء على ذلك يمكننا اعتبار ان مركز كتلة c.m. مثل هذه الأجسام يقع أيضاً في مراكزها الهندسية . (من الممكن بالطبع إيجاد مركز كتلة c.m. أي جسم غير متماثل هندسياً أو غير منتظم الكثافة).

الآن يمكننا استخدام مفهوم مركز الكتلة لتحديد معنى hΔ:

التغير في طاقة الجهد التثاقلي لجسم يعتمد على التغير في الموضع الرأسي لمركز كتلة ذلك الجسم.

إذن: بالقرب من سطح الأرض ، يمكن كتابة العلاقة:

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل