
المقذوف المنطق بزاوية
 المؤلف:
فريدريك بوش ، دافيد جيرد
المؤلف:
فريدريك بوش ، دافيد جيرد
 المصدر:
اساسيات الفيزياء
المصدر:
اساسيات الفيزياء
 الجزء والصفحة:
الفصل 2
الجزء والصفحة:
الفصل 2
 31-1-2016
31-1-2016
 17776
17776
المقذوف المنطق بزاوية
النوع العام الآخر من حركة المقذوفات هو حالة جسم مقذوف أو منطلق من مستوى الأرض بسرعة ابتدائية v0 في اتجاه يصنع زاوية 0θ فوق الأفقي. لنفرض مثلاً أن المدفع في الشكل (1أ) يطلق قذيفة. أثناء الحركة إلى اليمين ترتفع القذيفة تدريجياً إلى أن تصل إلى أقصى ارتفاع H فوق الأرض ثم تبدأ في الهبوط ، وفي النهاية ترتطم القذيفة بالأرض على مسافة ما من نقطة الانطلاق (تسمى أيضاً مدى المقذوف). وتخضع حركة القذيفة أيضاً لنفس المبادئ السابق مناقشتها في حالة المقذوفات الأفقية، ولكن الشروط الابتدائية هنا مختلفة. لنفحص هذا الموقف بالتفصيل.
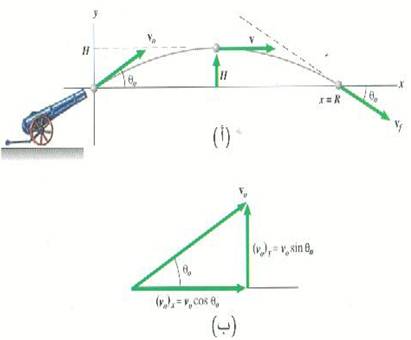
الشكل (1)
المركبة الأفقية للسرعة v0 هي v0 cos θ0 (شكل 1ب). وفي هذا الجزء من الحركة، تظل الحركة ثابتة لعدم وجود مركبة أفقية للعجلة.
إذن ، المعادلة التي تحكم الحركة الأفقية هي :
x = (v0 cos θ0)t
حيث افترضنا أن x = 0 عند نقطة الانطلاق.
أما المركبة الرأسية للسرعة باستثناء ان السرعة الابتدائية هنا v0 sin θ0 واتجاهها رأسي إلى أعلى. ومن ثم يمكن كتابة المعادلتين اللتين تصفان الحركة الرأسية مباشرة:

لاحظ ان مسار القذيفة متماثل حول نقطة منتصف الطيران. وأحد نتائج هذا التماثل هو أن الزمن اللازم لكي تصل القذيفة إلى أقصى ارتفاع يساوي نصف الزمن الكلي للطيران. والتماثل يعني أيضاً ان قيمتي مقدار السرعة التي ترتطم بها القذيفة بالأرض وزاوية الارتطام يظلان مساويين لقيمتيهما الابتدائيتين، باستثناء أن اتجاه السرعة يكون إلى الداخل بدلاً من الخارج.
يمكننا باستخدام المعادلتين السابقتين حذف الزمن t واشتقاق مثل هذه العلاقة وتسمى معادلة مسار القذيفة. وعليه فمن معادلة x نجد أن (x/(v0 cos θ0 = t ، وبالتعويض عن هذه الكمية في معادلة y نحصل على:
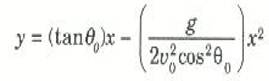
(وحيث استخدمنا حقيقة أن sin θ / cos θ = tan θ). هذه معادلة تربيعية على الصورة:
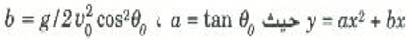 .
.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


