Generally speaking, a Green's function is an integral kernel that can be used to solve differential equations from a large number of families including simpler examples such as ordinary differential equations with initial or boundary value conditions, as well as more difficult examples such as inhomogeneous partial differential equations (PDE) with boundary conditions. Important for a number of reasons, Green's functions allow for visual interpretations of the actions associated to a source of force or to a charge concentrated at a point (Qin 2014), thus making them particularly useful in areas of applied mathematics. In particular, Green's function methods are widely used in, e.g., physics, and engineering.

More precisely, given a linear differential operator  acting on the collection of distributions over a subset  of some Euclidean space , a Green's function  at the point  corresponding to  is any solution of

(1)

where  denotes the delta function. The motivation for defining such a function is widespread, but by multiplying the above identity by a function  and integrating with respect to  yields

(2)

The right-hand side reduces merely to  due to properties of the delta function, and because  is a linear operator acting only on  and not on , the left-hand side can be rewritten as

(3)

This reduction is particularly useful when solving for  in differential equations of the form

(4)

where the above arithmetic confirms that

(5)

and whereby it follows that  has the specific integral form

(6)

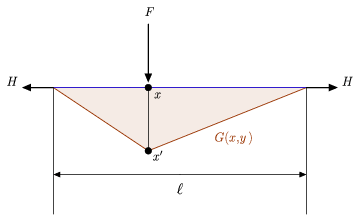
The figure above illustrates both the intuitive physical interpretation of a Green's function as well as a relatively simple associated differential equation with which to compare the above definition (Hartmann 2013). In particular, it shows a taut rope of length  suspended between two walls, held into place by an identical horizontal force  applied on each of its ends, and a lateral load  placed at some interior point  on the rope. Let  be the point corresponding to  on the deflected rope, suppose the downward force  is constant, say , and let  denote the deflection of the rope. Corresponding to this physical system is the differential equation

(7)

for  with , a system whose simplicity allows both its solution  and its Green's function  to be written explicitly:

(8)

and

(9)

respectively. As demonstrated in the above figure, the displaced rope has the piecewise linear format given by  above, thus confirming the claim that the Green's function  associated to this system represents the action of the horizontal rope corresponding to the application of a force .

A Green's function taking a pair of arguments  is sometimes referred to as a two-point Green's function. This is in contrast to multi-point Green's functions which are of particular importance in the area of many-body theory.

As an elementary example of a two-point function as defined above, consider the problem of determining the potential  generated by a charge distribution whose charge density is , whereby applications of Poisson's equation and Coulomb's law to the potential at  produced by each element of charge  yields a solution

(10)

which holds, under certain conditions, over the region where . Because the right-hand side can be viewed as an integral operator converting  into , one can rewrite this solution in terms of a Green's function having the form

(11)

whereby the solution can be rewritten:

(12)

(Arfken 2012).

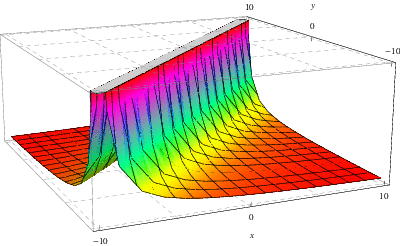
The above figure shows the Green's function associated to the solution of the - equation discussed above where here,  and , respectively , is plotted on the -, respectively -, axis.

A somewhat comprehensive list of Green's functions corresponding to various differential equations is maintained online by Kevin Cole (Cole 2000).

Due to the multitude of literature written on Green's functions, several different notations and definitions may emerge, some of which are topically different than the above but which in general do not affect the important properties of the results. As the above example illustrates, for instance, some authors prefer to denote the variables  and  in terms of vectors  and  to emphasize the fact that they're elements of  for some  which may be larger than 1 (Arfken 1985). It is also relatively common to see the definition with a negative sign so that  is defined to be the function for which

(13)

but due to the fact that this purely-physical consideration has no effect on the underlying mathematics, this point of view is generally overlooked. Several other notations are also known to exist for a Green's function, some of which include the use of a lower-case  in place of  (Stakgold 1979) as well as the inclusion of a vertical line instead of a comma, e.g., (Duffy 2001).

In other instances, literature presents definitions which are intimately connected to the contexts in which they're presented. For example, some authors define Green's functions to be functions which satisfy a certain set of conditions, e.g.,existence on a special kind of domain, association with a very particular differential operator , or satisfaction of a precise set of boundary conditions. One of the most common such examples can be found in notes by, e.g., Speck, where a Green's function is defined to satisfy  for points  and  for all points  lying in the boundary  of  (Speck 2011). This particular definition presents an integral kernel corresponding to the solution of a generalized Poisson's equation and would therefore face obvious limitations when being adapted to a more general setting. On the other hand, such examples aren't without their benefits. In the case of the generalized Poisson example above, for instance, each such Green's function  can be split so that

(14)

where  and  for the regular Laplacian  (Hartman 2013). In such situations,  is known as the fundamental solution of the underlying differential equation and  is known as its regular solution; as such,  and  are sometimes called the fundamental and regular parts of , respectively.

Several fundamental properties of a general Green's function follow immediately (or almost so) from its definition and carry over to all particular instances. For example, if the kernel of the operator  is non-trivial, then there may be several Green's functions associated to a single operator; as a result, one must exhibit caution when referring to "the" Green's function. Green's functions satisfy an adjoint symmetry in their two arguments so that

(15)

where here,  is defined to be the solution of the equation

(16)

Here,  is the adjoint of . One immediate corollary of this fact is that for self-adjoint operators ,  is symmetric:

(17)

This identity is often called the reciprocity principle and says, in physical terms, that the response at  caused by a unit source at  is the same as the response at  due to a unit force at  (Stakgold 1979).

The essential property of any Green's function is that it provides a way to describe the response of an arbitrary differential equation solution to some kind of source term in the presence of some number of boundary conditions (Arfken et al. 2012). Some authors consider a Green's function to serve roughly an analogous role in the theory of partial differential equations as do Fourier series in the solution of ordinary differential equations (Mikula and Kos 2006).

For more abstract scenarios, a number of concepts exist which serve as context-specific analogues to the notion of a Green's function. For instance, in functional analysis, it is often useful to consider a so-called generalized Green's function which has many analogous properties when integrated abstractly against functionals rather than functions. Indeed, such generalizations have yielded an entirely analogous branch of theoretical PDE analysis and are themselves the focus of a large amount of research.

REFERENCES:

Arfken, G. "Nonhomogeneous Equation--Green's Function," "Green's Functions--One Dimension," and "Green's Functions--Two and Three Dimensions." §8.7 and §16.5-16.6 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 480-491 and 897-924, 1985.

Arfken, G. B.; Weber, H.; and Harris, F. E. Mathematical Methods for Physicists, 7th ed.: A Comprehensive Guide. Orlando, FL: Academic Press, 2012.

Cole, K. D. "Green's Function Library." 2000. http://www.greensfunction.unl.edu/home/index.html.

Cole, K. D.; Beck, J. V.; Haji-Sheikh, A.; and Litkouhi, B. Heat Conduction Using Green's Functions, 2nd Edition. Boca Raton, FL: Taylor & Francis, 2011.

Duffy, D. G. Green's Functions with Applications. Boca Raton, FL: Chapman & Hall/CRC, 2001.

Hartmann, F. Green's Functions and Finite Elements. Heidelberg, Germany: Springer-Verlag, 2013.

Mikula, S. and Kos, A. "Using GNU Scientific Library for Temperature Computation in VLSI Systems." 2006. http://www.scalak.elektro.agh.edu.pl/files/mikula_kos_nti_green.pdf.

Qin, Q. "Green's Functions of Magneto-Electro-Elastic Plate Under Thermal Loading." In Encyclopedia of Thermal Stresses.Netherlands: Springer Netherlands, pp. 2096-2103, 2014.

Speck, J. "The Fundamental Solution and Green Functions." 18.152--Introduction to PDEs. MIT OpenCourseWare, 2011. http://math.mit.edu/~jspeck/18.152_Fall2011/Lecture%20notes/18152%20lecture%20notes%20-%207.pdf.

Stakgold, I. Green's Functions and Boundary Value Problems. New York: Wiley, 1979.