Airy Functions

There are four varieties of Airy functions: 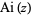, , 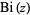, 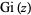and 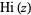. Of these,  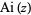and 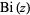 are by far the most common, with  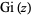and 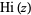 being encountered much less frequently. Airy functions commonly appear in physics, especially in optics, quantum mechanics, electromagnetics, and radiative transfer.

 

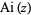 and 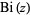 are entire functions.

 

A generalization of the Airy function was constructed by Hardy.

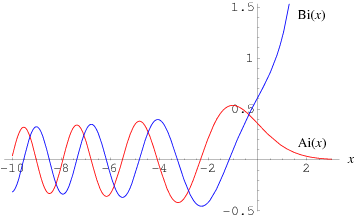
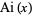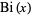The Airy function  and  functions are plotted above along the real axis.

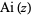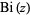The  and  functions are defined as the two linearly independent solutions to

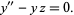(1)

(Abramowitz and Stegun 1972, pp. 446-447; illustrated above), written in the form

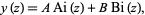(2)

where

			(3)
			(4)

where 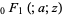 is a confluent hypergeometric limit function. These functions are implemented in the Wolfram Language as AiryAi[z] and AiryBi[z]. Their derivatives are implemented as AiryAiPrime[z] and AiryBiPrime[z].

For the special case 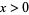, the functions can be written as

			(5)
			(6)
			(7)

where 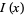 is a modified Bessel function of the first kind and  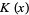is a modified Bessel function of the second kind.

Min   Max       Re       Im

Plots of 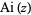 in the complex plane are illustrated above.

Min   Max       Re       Im

Similarly, plots of 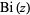 appear above.

The Airy 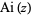 function is given by the integral

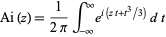(8)

and the series

			(9)
			(10)

(Banderier et al. 2000).

For ,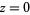

			(11)
			(12)

where 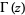 is the gamma function. Similarly,

			(13)
			(14)

The asymptotic series of 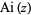 has a different form in different quadrants of the complex plane, a fact known as the stokes phenomenon.

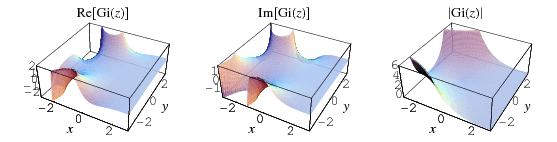
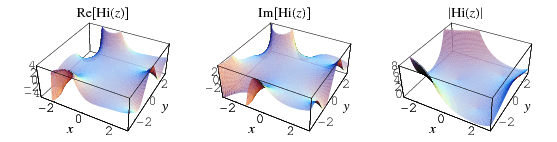
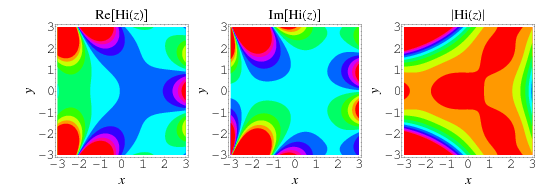
Functions related to the Airy functions have been defined as

			(15)
			(16)
			(17)
			(18)
			(19)
			(20)

where 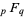 is a generalized hypergeometric function.

Watson (1966, pp. 188-190) gives a slightly more general definition of the Airy function as the solution to the Airy differential equation

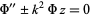(21)

which is finite at the origin, where 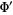 denotes the derivative 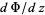, , 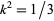and either sign is permitted. Call these solutions 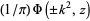, then

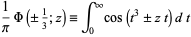(22)

			(23)
			(24)

where 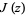 is a Bessel function of the first kind. Using the identity

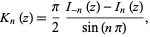(25)

where 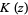 is a modified Bessel function of the second kind, the second case can be re-expressed

			(26)
			(27)
			(28)

---

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Airy Functions." §10.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 446-452, 1972.

Banderier, C.; Flajolet, P.; Schaeffer, G.; and Soria, M. "Planar Maps and Airy Phenomena." In Automata, Languages and Programming. Proceedings of the 27th International Colloquium (ICALP 2000) held at the University of Geneva, Geneva, July 9-15, 2000 (Ed. U. Montanari, J. D. P. Rolim, and E. Welzl). Berlin: Springer, pp. 388-402, 2000.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Bessel Functions of Fractional Order, Airy Functions, Spherical Bessel Functions." §6.7 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 234-245, 1992.

Sloane, N. J. A. Sequences A096714 and A096715 in "The On-Line Encyclopedia of Integer Sequences."

Spanier, J. and Oldham, K. B. "The Airy Functions Ai() and Bi()." Ch. 56 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 555-562, 1987.

Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.

مواضيع ذات صلة

Green,s Function

Valence

Simple Pole

Residue Theorem

Principal Part

ole

Critical Index

Complex Residue

Zeta Fuchsian

Zalcman,s Lemma

Wiener-Hopf Method

Weierstrass-Casorati Theorem