
Complex Modulus
 المؤلف:
Abramowitz, M. and Stegun, I. A.
المؤلف:
Abramowitz, M. and Stegun, I. A.
 المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
 الجزء والصفحة:
...
الجزء والصفحة:
...
 18-10-2018
18-10-2018
 1005
1005
Complex Modulus
The modulus of a complex number 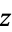 , also called the complex norm, is denoted
, also called the complex norm, is denoted 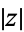 and defined by
and defined by
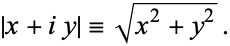 |
(1)
|
If 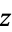 is expressed as a complex exponential (i.e., a phasor), then
is expressed as a complex exponential (i.e., a phasor), then
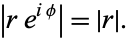 |
(2)
|
The complex modulus is implemented in the Wolfram Language as Abs[z], or as Norm[z].
The square 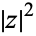 of
of 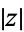 is sometimes called the absolute square.
is sometimes called the absolute square.
Let 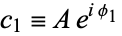 and
and 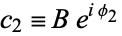 be two complex numbers. Then
be two complex numbers. Then
so
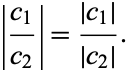 |
(5)
|
Also,
so
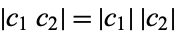 |
(8)
|
and, by extension,
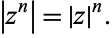 |
(9)
|
The only functions satisfying identities of the form
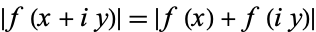 |
(10)
|
are 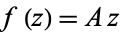 ,
, 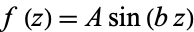 , and
, and 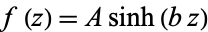 (Robinson 1957).
(Robinson 1957).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 16, 1972.
Krantz, S. G. "Modulus of a Complex Number." §1.1.4 n Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 2-3, 1999.
Robinson, R. M. "A Curious Mathematical Identity." Amer. Math. Monthly 64, 83-85, 1957.
 الاكثر قراءة في التحليل العقدي
الاكثر قراءة في التحليل العقدي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


