The basic rate equations of the multimode laser

In the preceding sections we have studied a laser, assuming that the atoms emit light only into a single mode. This is, of course, in contrast to the emission of atoms in conventional light sources where light is emitted, for instance, into all possible directions. As we mentioned above, a reason for mode selection is the different lifetimes of different kinds of photons. In this section we wish to study in more detail how mode selection in a laser is achieved. We shall see that simultaneous emission of photons into different modes can happen also. To this end we have to discuss the structure of the coefficient W which occurs in the laser equations more closely. So far we have taken this coefficient from Einstein's theory of absorption and emission of photons. As we shall show in detail in later chapters, W cannot be considered as constant for all kinds of photons. We wish to visualize how W looks like in reality and to derive its form in a heuristic fashion. (For its derivation from first principles. W stems of course, from the interaction of the light field with the atoms. If we consider a single standing light wave, e.g. in the form sin kx, it is quite clear that this light wave cannot have any

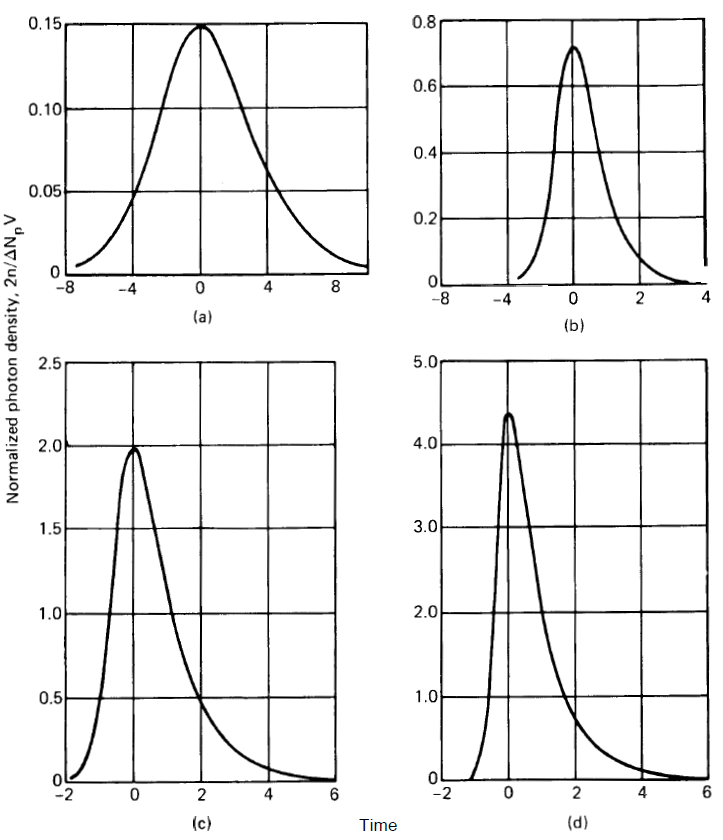
Fig. 1.1. Example of the time dependence of the emitted intensity of a Q-switching laser for various degrees of excitation.

interaction with an atom at the position x = 0 or at any of the other nodes of the sine wave. On the other hand we may expect a maximal interaction between atom and light wave if the sine function has its maximum. Because energy is exchanged between the atom and the light field we must assume that W does not depend on the field amplitude but rather on the intensity, i.e. on the absolute square of the field amplitude. Instead of a sine wave also other kinds of wave forms can be generated in the laser resonator. Denoting the corresponding wave forms by u_λ(x_μ) and using the ideas just mentioned we are led to assume the transition probability in the form

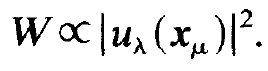    (1.1)

Because we shall deal with several wave forms we distinguish the u's by the index A, where A shall remind the reader of the wave-length. But in our present context it may also denote the various directions of propagation of a wave or its polarization, etc. x_μ denotes the space point where an atom is located. The individual atoms are distinguished by the index μ. In this sense W represents a transition rate caused by the interaction of the wave A and the atom μ. A further dependence of W on the light field and on the atomic quantities follows when we take into account the polarization of the light field and

Fig. 1.2. The interaction function W versus the spatial coordinate x along the laser axis. L is the distance between the mirrors of the laser resonator, x_μ the coordinate of atom μ. (a) x, coincides with an antinode; (b) x, coincides with a node.

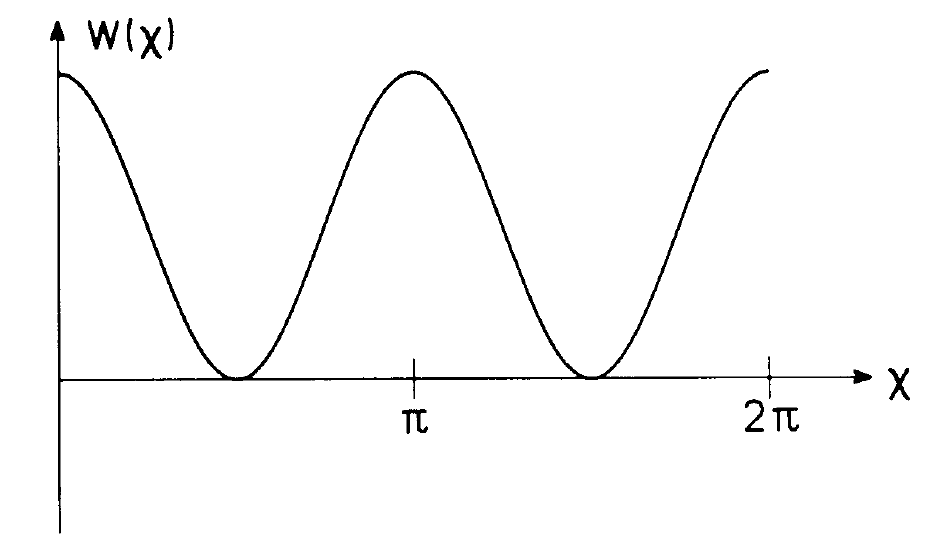
Fig. 1.3. This figure shows the dependence of the interaction function W on the angle x between atomic dipole moment and field polarization.

of the atoms. The electronic motion within the atoms can be described as that of oscillating dipoles. Here and in the following we shall assume for simplicity that the dipoles in the laser material are oscillating in the same direction. A light wave A having the direction of polarization e_λ can interact with an atomic dipole moment only to an extent in which the dipole moment of the atom 9 has its component in the direction of the polarization vector e_λ. Because only intensities play a role we are led to assume the dependence of W on the polarization in the form

   (1.2)

Finally we have to discuss how the positions of the mode frequencies relative to the frequencies of the optical transitions within the atoms enter into W. From now on we shall use in this book till its end the following notations for the circular frequencies of atoms and fields: circular frequency of the atomic transition 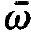, circular frequency of the light wave in the laser resonator o,. As is well known from experimental physics, the emission of atoms possesses a certain line shape. A single atom therefore does not uniformly radiate light in the region of its line-width into the individual frequencies but rather according to an intensity distribution. In case of a Lorentzian line the intensity of a light wave with frequency ⍵_λ and the central atomic transition frequency  is given by

    (1.3)

where we omitted a factor, I₀. Here y is the line-width or, more precisely speaking, the half width at half intensity. Now let us recall that W is the

Fig. 1.4. An illustration of the function W according.

rate with which an atom emits light into the mode A. Therefore we shall require that W is proportional to the expression (1.3) (fig. 1.4). In some cases we have to generalize (1.3). For instance, laser-active atoms in a solid may occupy different kinds of positions within the crystalline lattice. Due to their different positions the atoms have different central frequencies 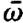 which we will have to distinguish by the atomic index μ. If there is a distribution of 6,'s over a certain frequency range, an inhomogeneous broadening is present. An inhomogeneous broadening is caused also in gases because of the Doppler shift due to the motion of the gas atoms. In the cases of homogeneous and inhomogeneous broadening we have to assume W in the form

    (1.4)

Because W depends on the mode A and on the laser atom μ under consideration, we attach the indices A and μ to W. Let us collect the individual conditions which we impose on W and let us anticipate the still lacking proportionality factor which we explicitly derive in a later chapter. W_λμ can then be written in the form

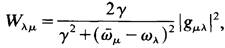    (1.5)

where we have used the abbreviation

   (1.6)

Evidently all factors within g_μλ are known from our above considerations except for the last one which can be derived by an exact quantum mechanical calculation only. We are now in a position to formulate the laser equations. We assume that there exists a certain set of modes in the laser resonator and we distinguish them by the index A. Each mode can be occupied with a certain number of photons n,. Because the lifetimes of different modes in the resonator can be different we introduce decay constants K_λ which in general will differ from each other. Because the individual atoms interact with the laser modes in a different way we have to consider the atoms individually. For simplicity we again consider the 2-level scheme leaving its extension to a 3-level scheme as an exercise to the reader. We denote the occupation numbers of the atom p in the states 1 and 2 by N_1,μ and N_2,μ, respectively. The corresponding inversion of atom p is described by d_μ = N_2,μ – N_1,μ. Generalizing we can immediately write down the laser equation for the mode A

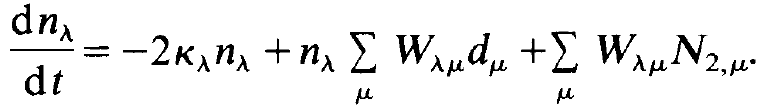    (1.7)

Though this equation was not derived exactly here (what we shall do later) its form is quite plausible. The temporal change of the number of photons of kind A is given by:

(1) losses (first term on the r.h.s.);

(2) the stimulated emission and absorption processes by the individual atom μ (first sum on the r.h.s.);

(3) a term representing spontaneous emission (second sum on the r.h.s.).

We shall omit this last term when we consider the laser process. A critical reader will quite rightly ask why no phase relations between the modes and the oscillating dipole moments of the electrons of the atoms are taken into account. In fact, (1.7) implies an approximation whose meaning we shall study in a later chapter. Eq. (1.7) can be obtained only if phase relations are neglected which is allowed in many cases but definitely not always. Indeed, very important effects in the laser, such as mode locking, are due to specific phase relations. The rate equations for the individual atom μ must take into account pump and relaxation processes and, in addition, the effect of stimulated emission and absorption. Because not only a single kind of photons but various kinds of photons are emitted, all the photon numbers must be taken into account. On account of these ideas we obtain the rate equations for the atom μ

    (1.8)

and

   (1.9)

By adding (1.8) to (1.9) we obtain the conservation law for the total occupation number of the atom μ

and thus

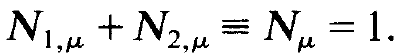     (1.10)

Because we are dealing with a single atom, we have put N_μ = 1. In a way analogous to the single mode laser, we may derive an equation for the inversion d_μ = N_2,μ – N_1,μ from (1.8) and (1.9),

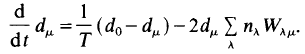(1.11)

Eqs. (1.6) and (1.11) are the basic laser equations which we wish to discuss now.