Time-Dependent Harmonic Oscillator I

Consider a simple harmonic oscillator in one dimension:

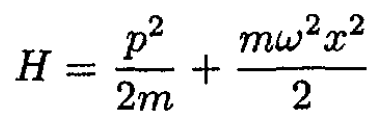(i)

At t = 0 the wave function is

(ii)

where ψ_n (x) is the exact eigenstate of the harmonic oscillator with eigenvalue hω(n+1/2).

a) Give Ψ(x, t) for t ≥ 0.

b) What is the parity of this state? Does it change with time?

c) What is the average value of the energy for this state? Does it change with time?

SOLUTION

a) At times t ≥ 0 the wave function is

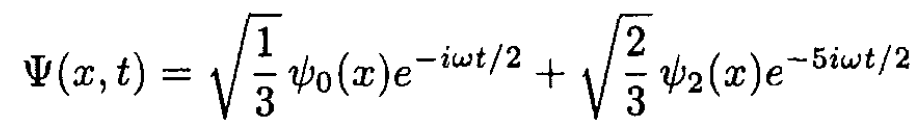(1)

b) The state Ψ(x, t) has even parity: it remains the same if one replaces x by –x, since ѱ_2n(-x) = ѱ_2n(x).  This is true for all times.

c) The average value of the energy is

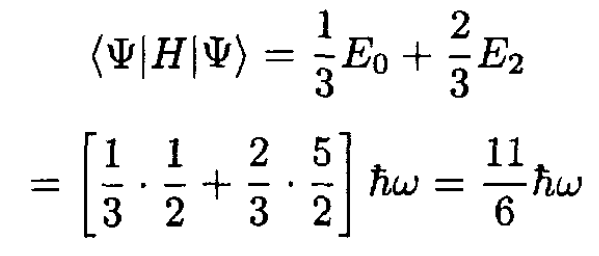(2)

which is independent of time.