البيروني

محمد بن احمد، ابو الريحاني البيروني الخوارزمي، فيلسوف رياضي مؤرخ، من اهل خوارزم، ولد في اليوم الثاني من شهر ذي الحجة عام 362هــ في قرية من ضواحي مدينة كات عاصمة دولة خوارزم من عائلة مغمورة، ويقول هو عن نفسه : انا بالحقيقة لا اعرف نسبتي ولا اعرف من كان جدي، ويذكر ابن ابي اصبعيه في ترجمته، انه منسوب الى بيرون في السند، وكان مشتغلا بالعلوم والحكمة، فاضلا في علم الهيئة والنجوم، وله نظر جيد في صناعة الطب، وكان معاصرا للشيخ الرئيس (ابن سينا) وبينهما مباحثات ومراسلات.

درس محمد في شبابه علوما شتى ولغات عديدة، فكان يعرف اللغة الخوارزمية والفارسية والعربية والسنسكريتية والسريانية واليونانية، وكان اول معلم تتلمذ عليه يوناني لم تذكر المصادر اسمه، وكان محمد يجمع له اصنافا كثيرة من النباتات وبذورها، ويسأله مستفهماً باحثا، فيسجلها له استاذه اليوناني شارحا خواصها وصفاتها وفوائدها.

استقر ابو الريحان في بلاط السلطان مسعود، الغزنوي، وما لبث ان اهدى اليه رسالته في علم الفلك والرياضيات وهي الرسالة المعنونة القانون السعودي في الهيئة والنجوم، والملفت انه وفي السنة نفسها التي اهدى فيها هذه الرسالة الضخمة كتب رسالة ثانية في علوم الهندسة والحساب والنجوم واسماها التفهيم لأول صناعة التنجيم وقد اعتبر المؤرخون ان قانون المسعودي اكبر موسوعة في الفلك والهندسة والجغرافية، ويذكر ان البيروني لما انتهى من وضع هذا السفر الجليل حمله الى السلطان مسعود فاراد ان يجزيه على هذا الجهاد الكبير بعض ما يستحقه، فوجه اليه ثلاثة جمال تنوء باحمالها من نقود الفضة، فردها ابو الريحان اليه قائلا : انه يخدم العلم للعلم لا للمال.

اما كتابه الكبير الثاني تحديد نهايات الاماكن لتصحيح مسافات المساكن فقد حققه المستشرق السوفيتي الدكتور بولجاكوف واعانه في الدكتور امام ابراهيم احمد في ما يتعلق منه بعلم الفلك، ثم كتابه الجماهر في معرفة الجواهر، الذي حققه المستشرق الروسي كرموكوف، وقام مستشرق وكيماوي روسي آخر بتحقيق مؤلفاته في علوم الصيدلة والطب، ويعد ابو الريحان فلاكيا شهيرا يجمع على معرفته بهذا العلم الغربيون والعرب، وهو في الجغرافية الجيولوجية علما كبيرا كما في التاريخ الذي بدا فيه مؤرخا مدققا واسع الاطلاق شامل المعرفة قادرا على الاستقراء والاستنتاج، وهو في علم الرياضيات من اساطينه اخذ عنه نيوتن وغريغوري كثيرا من القوانين الرياضية.

وقد كان تاريخ وفاته موضع خلاف بين المترجمين لحياته؛ على ان الاغلب انه توفي بعد سنة 441 هـ (1050م) ويذكر ان ابا الريحان لم يكف لحظة عن التفكير في المسائل العلمية حتى وهو على فراش الموت، وقد روى ياقوت الحموي النيسابوري ان قاضيا من اصحاب البيروني قال : دخلت على ابي الريحان وهو يجود بنفسه وقد حشرج نفسه وضاق به صدره، فقال لي في تلك الحال : كفي قلت لي يوما حساب الجدات الفاسدة؟ فقلت له اشفاقا عليه : أفي تلك الحالة؟/ قال لي : يا هذا، اودع الدنيا وانا اعلم بهذه المسالة، الا يكون خيرا من ان اخليها وانا جاهل بها؟ فاعدت ذلك عليه وحفظه – وعلمني ما وعد، وخرجت من عنده وانا في الطريق فسمعت الصراخ.

وقد خلف البيروني اكثر من مائة وثمانين كتابا ضاع الكثير منها، ونشر هو نفسه فهرسا باسماء مائة وثلاثين منها وذلك في مؤلفاته رسالة في فهرس كتب محمد زكريا الرازي بالإضافة الى مؤلفاته اللاحقة التي اتمها بعد ان كتب فهرسه ونشر بعضها وهو في قيد الحياة، والبعض الاخر نشره بعد وفاته عدد من العلماء منهم ابو نصر منصور بن علي بن عراق، استاذ البيروني واحد ثلاثة ينسب اليهم اكتشاف قانون الجيوب للمثلثات الكروية، وابو سهل عيسى بن يحيى المسيحي، استاذ ابن سينا، وابو علي الحسن بن علي الجيلي.

اما مؤلفاته الرياضية فهي :

• كتاب في افراد المقال في امر الظلال.
• تذكره في الحساب والعد بأرقام السند والهند.
• في استخراج الكتاب واضلاع ما وراءه من مراتب الحساب.
• في ان رأي العرب في مراتب العدد اصوب من راي الهند فيها.
• في راشيكت الهند.
• ترجمة ما في براهم سدهاند من طرق الحساب.
• في تسطيح الصور وتبطيح الكور.
• مقالة في استخراج الاوتار في الدائرة بخواص الخط المنحني فيها.
• المقالة الثانية من القانون المسعودي.
• مقالة في ان لوازم المقادير لا الى نهاية قريبة من امر الخطين اللذين يقربان ولا يلتقيان في الاستبعاد.
• جمع الطرق السائرة في معرفة اوتار الدائرة.
• رسالة في جدول الدقائق.
• رسالة في حل شبهة عرضت في الثالثة عشرة من كتاب الاصول.
• كتاب في مبادئ الهندسة.
• استيعاب في تسطيح الكرة.
• رياضة الفكر والعقل.
• ترجمة كتاب في اصول الهندسة لاقليدس الى لغة الهند.
• رسالة ابي نصر في جواب مسائل الهندسة.
• رسالة في الابعاد والاجرام (تحتوي على احد عشر بابا، منها مساحة الارض وبعد القمر من الارض ومقدار جرم القمر من جرم الارض، الى غير ذلك).

البيروني الرياضي :

استلقى ابو الريحان علومه الرياضية من التراث الإغريقي والتراث الهندي، ثم اضاف اليهما من مجهوداته في البحث وقد نهج حقيقة في التوصل الى آرائه واقرارها منهج الدرس والبحث والاستقصاء، فاعتمد على قدر ما كان يتاح الاعتماد عليه في زمنه من لتعرف على العلوم الرياضية من العلماء المتقدمين او من العلماء المعاصرين، وبذلك نحا المنحنى الحسي لا الإشراقي الذي كان سائدا عند اهل التصوف في عمره، والذين كانوا يسلكون الى المعرفة سبيل الرياضة والمجاهدة، ويذهبون الى ان المعرفة تستفاد ولا تكتسب لا بفعل من العقل بل برياضة النفس بالزهد عن متاع الحياة والانصراف عن شواغل الحس والانقطاع الى التأمل الباطني، حتى يصل طالب المعرفة الى حال يذهل فيها عن الوجود الخارجي ويغيب فيها عن نفسه فتشرق عليه معرفة يفيض الهي.

وقد اعتمد ابو الريحان البيروني في دراساته على البحوث الرياضية التي كانت امتدادا لتراث اقليدس وابولونيس وارخميدس وهيرمن، يضاف اليها ما استحدث من نظريات وابحاث، من مثل :

1. مساحة المجسم المكافئ، للشيخ ابي سهل ويجن بن رستم القوهي (ت 390هـ).
2. كيفية تسطيح الكرة على شكل الاسطرلاب، لاحمد بن محمد الحسين الصفائي (ت380هـ).
3. رسالة في ان الاشكال كلها من الدائرة، لنصر بن عبدالله (ت 400 هـ).
4. رسالة في المقادير المشتركة والمتباينة، لابن البغدادي.
5. كتاب الجبر والمقابلة، لمحمد بن موسى الخوارزمي (ت 259هـ).
6. رسالة في شكل القطاع، لأحمد بن محمد بن عبدالجليل بن محمد السجزي (415هـ)
7. رسالة في إقامة البرهان على الدائرة، لأبي الوفاء محمد البوزجاني (ت388هـ).

لم يكن وصول البيروني الى هذه القوانين من قبيل المصادفة والتخمين، بل كان نتيجة البحث الدقيق في الجداول الرياضية السابقة وطرق استخدامها، فقد رأى ان الفترات المتساوية بين الزوايا لا تقابلها تغيرات متساوية في النسب المثلثية، وتأكيداً لصحتها اثبتها بالطرق الهندسية وكان في ذلك حافز له في البحث عن مخرج للوصول الى ادق القيم حين استعمال الجداول المثلثيثة وتعميم هذا على جميع الجداول الرياضية، وقد نهج في سبيل تبيان ذلك مسلكين، الاول اخذ فترات صغيرة قدر الامكان بين قيم المتغير (الزوايا) وعمل جدول على هذا الاساس، وقام بحساب جداول للجيوب لكل ربع درجة بدلا من الجداول المعروفة انذاك والتي كانت محسوبة لكل درجة كاملة، وقد كان يأمل ان يعلمها لكلا دقيقة قوسية لولا امتداد الوقت وكثرة الحسابات، وهو يقول في هذا الوجه : فلهذا لو لم يتعذر تدقيق العمل لطوله، لكان تحليل الجيوب الى دقائق اجزاء الاجزاء الى التي لم نستعملها، وكان الاولى بنا ان نفعله، لان مدار امور هذه الصناعة عليها ومرجع الزيجات اليها وكانت حساباته في الدقة الى درجة، ان جداوله كانت صحيحة الى الرقم السابع او الثامن العشري.

اما المسلك الثاني، فهو تحسين طريقة استعمال هذه الجداول، وهذا ما ادى بها الى استنباط قانون الاستكمال مقربا بطريقة هندسية بسيطة وكانت فكرته – كما يلي- حسب علوم الاصطلاح الحديث.

ونشير الى طريقة التقريب المتتابع المعروفة لدى الرياضيين في الوقت الحاضر والتي استخدمها البيروني لا يجاد طول وتر في دائرة يقابل زاوية قدرها 40 درجة عند المركز (أي – الدورة الكاملة)، وكان هدفه ايجاد الاوتار التي تقابل من الدورة الكاملة ثالثها وربعها وخمسها.. وهكذا، وذلك تمهيداً لحساب قيم هذه الاوتار فيما عدا وترى السبع والتسع، كما استنتج قوانين لوتر مجموع زاويتين او الفرق بينهما او قيمة نصف الزاوية وقد بدا البيروني طريقة التقريب المتتابع هذه فاخذ وترى الخمس والسدس (وهما يقابلان 72 درجة و 60 درجة) واستخرج وتر الفرق بينهما وتر (12 درجة)، ومن وتر السدس ايضا باستعمال قانون التنصفي وصل الى وتر 30، ثم استخدم قانون المجموع  لايجاد وتر (30+12) أي 42 وهو قريب من40، والخطوة التالية هي تصنيف 42 مرتين ومن ذلك وصل الى وتر (30- 10)، فلما اخذه مع وتر 30 درجة حصل على وتر 30 درجة 40 درجة وبذلك اقترب كثيرا من 40درجة، وبمتابعة هذه الخطوات الاخيرة نفسها امكنه الاقتراب من وتر 40درجة المطلوب قدر الامكان، ولما اتبع البيروني هذه الطريقة وصل الى وتر 40درجة صفر دقيقة، صفر ثانية، صفر ثالثة، 24 رابعة، وبعد رابع وستين عملية حسابية لايجاد الجذر التربيعي عدا طرقه الاخرى التي اوصلته الى معادلات من الدرجة الثالثة قام بحلها بطرق المحاملة والخطا حتى توصل الى قيمة صحيحة حتى الرقم السادس العشري.

البيروني الرياضي والتراث الهندي :

اطلع البيروني على كتب حكماء الهند، وقد درس العلوم الرياضية الهندية ولكنها لم ترق له، لانه وجدها تميل دوما الى الخرافات فتختلط العلوم الاصلية بها، على عكس كتب الاغريق المنستقة، والتي قال عنها انها تسير على نهج علمي بعيد عن الخيال الخرافي حيث قال في ما في الهند من مقولة : لم يك للهند امثالهم – أي علماء الاغريق – ممن يهذب العلوم، فلا تكاد تجد لذلك لهم خاص كلام الا في غاية الاضطراب وسوء النظام ومشوبا في آخره بخرافات العوام.. ثم يقول : اني اشبه ما في كتبهم الحساب ونوع التعاليم الا بصرف مخلوط بخزف او بدر ممزوج ببعر او بمهى مقطوب بحصى، والجنسان عندهم سيان.

لكنه مع هذا لا ينكر فضل الهنود في ادخال الصفر والاعداد، فنسمعه يقول في مقالة ما للهند : قال برهمكوبت : اذا اردتم ان تكتبوا  واحد فعبروا عنه لكل شيء هو واحد كالارض والقمر، وعن الاثنين بكل ما هو اثنان كالسواد والبياض، وعن الثلاثة بكل ما يحوي ثلاثة، وعن الصفر باسماء السماء وعد الاثني عشر باسماء الشمس، وقد اودعت الجدول ما كنت اسمعه منهم فانه اصل عظيم من حل زيجاتهم ومنها الصفر ستون كما وهما النقطة، ثم يبتكر البيروني برهانا لمساحة الشكل الرباعي الدائري على طريقة الهند وليس نقلاً لبرهان برهمكوبت :

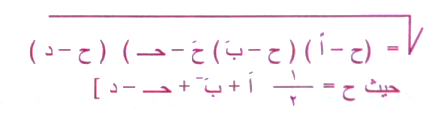
البيروني والنسبة التقريبية ط :

توصل البيروني في الباب الخامس من القانون السعودي الى ايجاد ط برسم مضلع منتظم داخل الدائرة بعدد من الاضلاع = 180 فوجدها = 3.1217466، مع ارخميدس العالم السكندري (عام 225 ق.م) وجد ان ط اقل من 3 1/7 واكبر من 3  10/71 لأنه رسم مضلعا ذا 96 ضلعا لتحقيق هذا الغرض.

وبرهمكوبت استخدم العدد 3 من الوجهة العملية والعد  كقيمة حقيقية لها.

وأيده في نتيجة هذه ماهافيرا (850م)، وسريدها (1020م).

وفي الصين استخدم شانج هونج (125م) العدد  كقيمة لها.

اما شونج شيح (470م) فقد استخدم دائرة قطرها عشرة اقدام فوصل الى قيمة ط ما بين 3.1415926.3.1415927.

ونشير هنا الى ان ادق قيمة صل اليها العلماء العرب – بالنسبة الى قيمة ط – هي التي وصل اليها جميشد غياث الدين الكاشي بعد البيروني بثلاثة قرون تقريبا وهي : ط = 3.141592653535898732.

حساب المثلثات عند ابي الريحان :

عرف العرب وتر ضعف الزاوية كمقياس لها عن الغريق، وعن الهنود وعرفوا نصف هذا الوتر، وكان الهنود يطلقون عليه اسم جيبا أي وتر، وقد استحسن العرب هذا اللفظ ومعناه فتحة الجلباب لقربه من اللفظ السنسكريتي جيفا فأطلقوا على نصف وتر ضعف الزاوية اسم الجيب، ويقول البيروني في المقالة الثالثة من القانون المسعودي، ما نصه : ان الصناعة اذا اريد اخراجها الى الفعل بمزاولة الحساب فيها، فالأعداد مفتقرة الى معرفة اوتار قسي الدائر، فلذلك سمى اهلها كتبها العلمية الزيجات من الزيق الذي هو بالفارسية الوتر، وسموا انصاف الاوتار جيوبا، وان كان اسم الوتر بالهندية جيبا ونصفه جيبارد، ولكن الهند اذا لم يستعملوا غير انصاف الاوتار اوقعوا اسم الكل على النصف تخفيفا في اللفظ.