


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 2-8-2016
Date: 26-8-2016
Date: 14-8-2016
|
Charge and Dielectric
A charge e is situated at the point x = h > 0, y = z = 0 outside a homogeneous dielectric which fills the region x < 0 (see Figure 1.1).

Figure 1.1
a) Write the electric fields E(0+, y, z) and E(0-, y, z) just outside and just inside the dielectric in terms of the charge e and surface charge density σb of bound charges on the surface of the dielectric.
b) Express σb in terms of E(0-, y, z). Denote by the dielectric constant of the dielectric.
c) By using the equations obtained in (a) and (b), show that
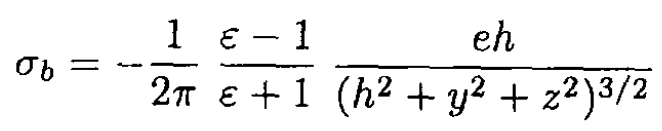
d) Calculate the electric field E' due σb to at the position (h, 0, 0) of the charge e. Show that it can be interpreted as the field of an image charge e' situated at the point (-h, 0, 0).
e) Show that the charge experiences the force

SOLUTION
a) The electric fields just above and below the dielectric due to the charge e and the surface charge σb(y, z) are, respectively,
 (1)
(1)
 (2)
(2)
b) From D = E + 4πP = εE, we have for the polarization P and its normal component to the boundary Pn
 (3)
(3)
c) Using (2) in (3), we have
 (4)
(4)
So
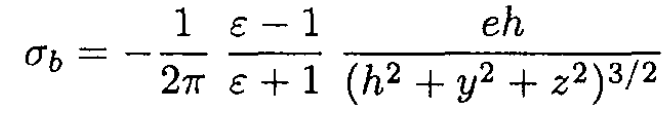 (5)
(5)
d) The field at the position of the charge due to the surface charge σb is
 (6)
(6)
where dA is the area. We can rewrite this integral in cylindrical coordinates:
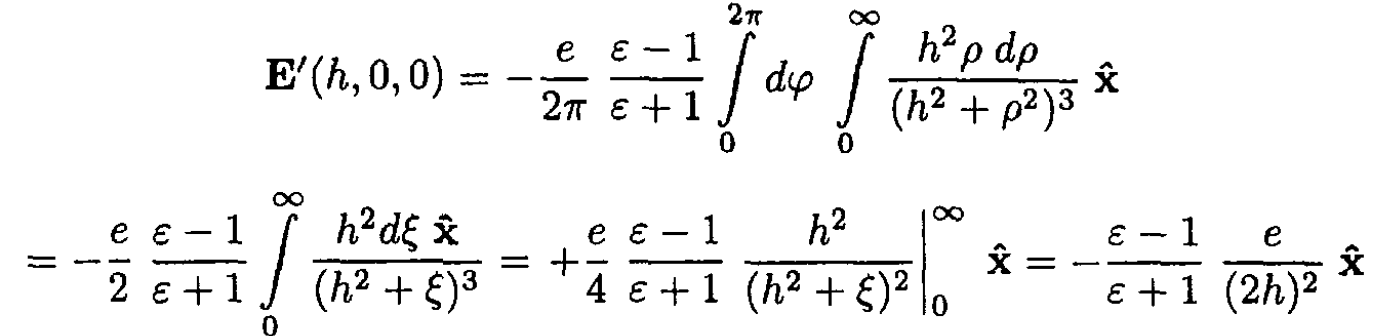 (7)
(7)
This can be interpreted as an image charge
 (8)
(8)
at a distance 2h from the charge e (see Figure 1.2).

Figure 1.2
e) The force on the charge e is
 (9)
(9)



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
لتعزيز التواصل مع الزائرات الأجنبيات : العتبة العلويّة المقدّسة تُطلق دورة لتعليم اللغة الإنجليزية لخادمات القسم النسويّ
|
|
|