OUTPUT   POWER

Using the results of previous sections in which we have derived expressions for inversion, gain, and saturation, we may now formulate an expression to predict the amount of power that we can expect from a particular laser system. We stated that at threshold conditions, gain must equal loss in the laser. In terms of a round trip through the laser (i.e., two passes through the gain medium),

round-trip gain = round-trip loss

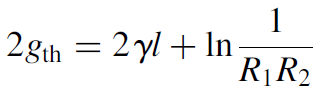 (1.1)

where gth is the threshold gain, γ the absorption coefficient for the lasing medium (in m^-1), and l the length of the gain medium. If however, gain exceeds the threshold value, it must saturate down to reach an equilibrium point once again. The intensity of light inside the cavity grows in the process, and a usable output beam appears as a fraction of that intracavity intensity (that fraction being 1- R_OC, where R_OC is the reflectivity of the output coupler; the other cavity mirror is assumed to be 100% reflecting in this case). We must substitute the value for saturated gain (with intensity used in place of photon flux) for gth in equation (1.1), to obtain

   (1.2)

where the 2 in front of the intensity in the demoninator of the saturated gain equation denotes that intensity in the cavity originates from a flux of photons moving toward one mirror and a second flux moving toward the opposite mirror (so that I toward one mirror is actually I_cavity/2). This may now be solved for I:

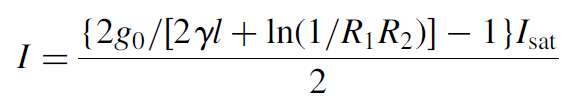 (1.3)

where g₀ is the unsaturated (single-pass) gain of the laser (proportional to inversion ΔN ) and I_sat is the saturation intensity. As expected, the unsaturated gain g₀ is multiplied by 2 since it is usually expressed as a single pass gain (determined by experimental means using a method similar to that, in which g = αl, where α, the gain coefficient in units of m^-1, is multiplied by the length of the gain medium in a single pass). Multiplying this figure by 2 gives the round-trip gain required for this expression.

       Expression (1.3) gives us I, the intensity of light inside the laser cavity. We may further express this intensity as output power by multiplying by the area of the laser beam inside the cavity (assuming that t is consistent throughout) since power = intensity × area as well as the transmission of the output coupler (1 2 R). Since unsaturated gain may be calculated or measured experimentally, we can calculate the maximum power available from a given laser.

Example 1.1 Red He Ne Laser Tube Consider a red He Ne laser tube with an experimentally measured unsaturated gain of 0.135 m^-1. If the output coupler has 99% reflectivity, the high reflector is 100% reflective, the absorption of the medium is 0.01 m^-1 (with a tube length

Figure 1.1. Power output as a function of OC reflectivity (generalized).

of 27.5 cm), and I_sat determined experimentally, the output power of the laser may be calculated as follows:

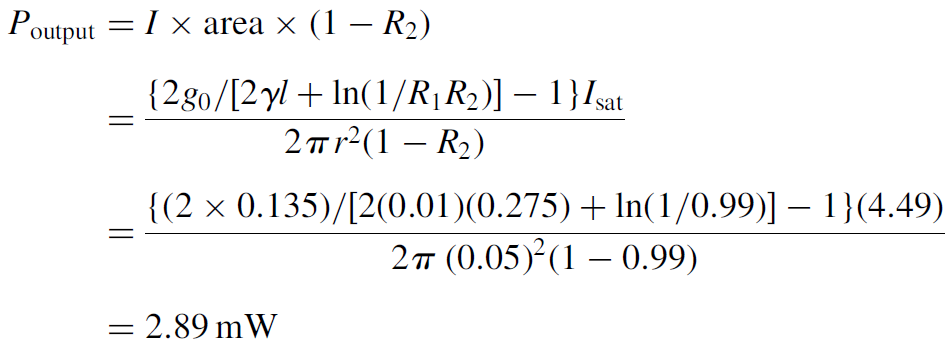
In the laboratory, an optimized laser of this type has been demonstrated to have an output of approximately 3.0 mW, in good agreement with this calculation.

         Finally, we may use the expression for intensity to determine the optimal value of output coupling for a given laser. For any given laser we can plot the expected power output as a function of the reflectivity of the output coupler, which renders a plot like that of Figure 1.1. For this particular laser the optimal value for the output coupler is 3% reflectivity. The plot also shows that as expected, there is a minimum value of reflectivity for the output coupler at which the laser ceases oscillation entirely.