حساب المحددات بطريقة الاختزال الصفي:

سنبين في هذا البند كيفية إيجاد المحددات بطريقة اختزال المصفوفات صفياً إلى الشكل المدرج الصفي. هذه الطريقة مهمة لكونها تجنينا الإطالة عند استخدام دالة المحدد.

مبرهنة (1-1):

لتكن A مصفوفة مربعة

1. إذا احتوت A على صف (أو عمود) جميع عناصره أصفاراً فإن det(A) = 0

2. det (A) = det (A^T)

البرهان:

1. لما كان حاصل الضرب البسيط ذي الإشارة الموجية أو السالبة من A يحتوي على عامل واحد من كل صف وعامل واحد من كل عمود، فإن كل حاصل ضرب بسيط من الضروري أن يحتوي على عامل قيمته صفر من الصف الصفري أو العمود الصفري. لذا فإن كل ضرب بسيط ستكون قيمته صفر ومن ذلك نستنتج بان det (A) الذي هو مجموع حواصل الضرب البسيط ذات الإشارة الموجبة أو السالبة ، يساوي صفر.

2. البرهان غير مطلوب لأنه يعتمد على حقول أخرى يجب معفرتها ولكن نود أن نذكر أن حاصل الضرب البسيط يحتوي على عامل واحد من كل حواصل الضرب البسيط. بموجب بعض مبرهنات التبديلات يمكننا أن نبرهن أن A منقولتها A^T لها نفس حواصل الضرب البسيط ذات الإشارة الموجية أو السالبة.

ملاحظة:

بواسطة المبرهنة أعلاه يمكننا استبدال كلمة صف بكلمة عمود في جميع المبرهنات المتعلقة بالمحدد.

مبرهنة (2-1):

إذا A مصفوفة مثلثية (عليا، سفلى أو قطرية) فإن محدد A هو عبارة عن حاصل ضرب العناصر الواقعة في القطر الرئيسي، أي:

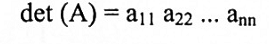
البرهان:

لغرض تبسيط البرهان نأخذ الحالة عندما A سعتها 4 ×4  وبنفس الطريقة نبرهن الحالة العامة عندما سعة A هي n × n نفرض:

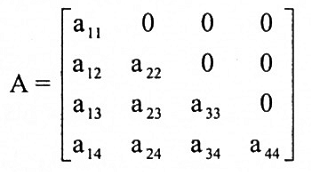
حاصل الضرب البسيط الوحيد في A الذي لا يساوي صفر هو a₁₁a₂₂a₃₃a₄₄ ولإثبات ذلك، نأخذ الضرب البسيط a₁j₁ . a₂j₂ ….. a_nj_n.

بما أن a₁₂ = a₁₃ = a₁₄ = 0 فيجب أن يكون j₁ يساوي 1 لكي يكون لدينا ضرب بسيط لا يساوي صفر. إذا كان j = 1 فيجب أن يكون j₂ ≠ 0 لعدم وجود عاملين من نفس العمود. إضافة لذلك لما كان a₂₃ = a₂₄ = 0 فيجب أن يكون j₂ = 2 لكي نحصل على ضرب لا يساوي صفر لكن a₁₁a₂₂a₃₃a₄₄ موجبة فإننا سنحصل على:

مثال(1):

إذا كانت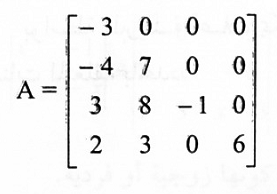                                                

فإن:

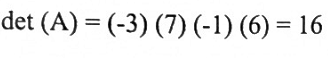
تأثير العمليات الصفية البسيطة على المحددات:

مبرهنة (1-3):

لتكن A مصفوفة سعتها n x n فإن

1. إذا كانت  B  مصفوفة ناتجة من حاصل ضرب أحد صفوف (اعمدة )A بكمية ثابتة k فإن:

                                                          Det (B) = k det (A)

2. إذا كانت B مصفوفة ناتجة من تبادل صفين (عمودين) أحدهما مكان الآخر في المصفوفة A فإن:

                                                          Det (B) = - det(A)

3. إذا كانت B مصفوفة ناتجة من جمع مضاعف أحد صفوف (أحد أعمدة) A إلى صف آخر (عمود آخر) فإن:

                                                          Det (B) = det(A)

البرهان:

يمكن برهان المبرهنة اعلاه باستخدام الصيغة (1) في (طريقة حذف كاوس) لحساب المحددات المطلوبة ومن ثم التأكد من صحة المتساويان.

مثال (2): نوضح البرهان بمثال عندما سعة A هي 3x3

وللزيادة في التوضيح نأخذ المثال:

مثال (3):

عليه فإن: det (B) = 2 det (A)

وهكذا تتحقق الخاصية الأول من المبرهنة (1.3).

وبنفس الأسلوب نستطيع تحقيق الخواص الأخرى.

مبرهنة (1-4):

1. لتكن E مصفوفة ناتجة من ضرب أحد صفوف I_n بثابت مثل k فإن: det (E) = k

2. إذا كانت E ناتجة من تبديل صفين من صفوف I_n بكمية ثابتة وإضافته إلى صف آخر من I_n فإن det (E) = 1.

3. إذا كانت E ناتجة من ضرب احد صفوف I_n بكمية ثابتة وإضافته إلى صف آخر من I_n فإن det(E) = 1

البرهان:

بموجب المبرهنة (1-3) وتعويض A = I_n ستصبح B مصفوفة بسيطة.

مثال(4):

المحددات الآتية توضيح المبرهنة (1-4):

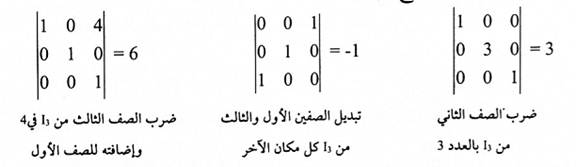
مبرهنة (1-5):

إذا كان أحد صفوف المصفوفة المربعة A (او أحد أعمدتها) هو عبارة عن مضروب صف آخر من صفوفها (او عمود من أعمدتها) فإن:

                                                Det (A) = 0                           

البرهان:

نفرض أن أحد صفوف (أعمدة) المصفوفة المربعة A عبارة عن مضاعف مناسب لصف آخر فيمكن الحصول على صف (عمود) جميع عناصره أصفار، لكن جمع مضاعف أحد الصفوف إلى الآخر( مضاعف عمود الى الآخر) لا يغير المحددة لذا من مبرهنة (1) (2-2-1) يجب ان نحصل على:

                                                                             Det(A) = 0

مثال(5):

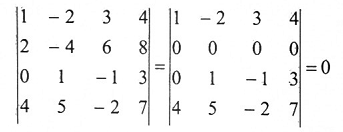
لاحظ أن الصف الثاني هو عبارة عن الصف الاول مضروب في 2، للحصول على الصف الصفري نضيف ضرب الصف الأول في -2 إلى الصف الثالث.

ملاحظة:

من الممكن استخدام الشكل المدرج الصفي للحصول على المحددات وذلك بتحويل المصفوفة المعينة إلى مصفوفة مثلثية عليا باستخدام عمليات الصف البسيطة ومن ثم نجد المحدد للمصفوفة المثلثية العليا(مبرهنة 1-2).

مثال (6):

احسب det (A) حيث                               

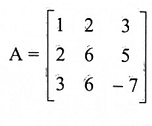
الحل: نحول المصفوفة A للشكل المدرج الصفي ومن ثم نعتمد على المبرهنة (2-2-2) للحصول على محدد A.