

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
أنظمة المعادلات الخطية والمصفوفات -المصفوفات البسيطة، طريقة إيجاد معكوس المصفوفة A-1
المؤلف:
علي جاسم التميمي
المصدر:
مقدمة في الجبر الخطي
الجزء والصفحة:
56-63
13-3-2016
42174
المصفوفات البسيطة، طريقة إيجاد معكوس المصفوفة A-1:
سوف نستعرض في هذا البند تنسيقاً بسيطاً لإيجاد معكوس المصفوفة ونناقش بعض الخواص الأساسية للمصفوفات القابلة للانعكاس.
تعريف (1-1):
تمسى المصفوفة المربعة A مصفوفة بسيط إذا أمكن إيجادها من المصفوفة المحايدة In باستخدام عملية صف بسيطة واحدة.
مثال (1):


عند ضرب مصفوفة A من جهة اليسار بمصفوفة أولية مثل E، فإن تأثير ذلك يكون معادلة لإجراء عملية صفية على A.
مثال (2):
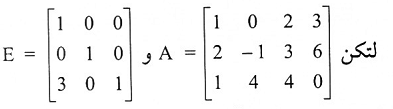
مصفوفة بسيطة حصلنا عليها من ضرب الصف الأول في 3 وإضافة حاصل الضرب إلى الصف الثالث من المصفوفة I3.
إذن:
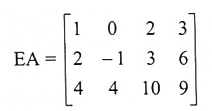
وهذا الشكل معادل للمصفوفة الناتجة من إضافة 3 أضعاف الصف الأول في A إلى الصف الثالث فيها.
ملاحظة:
إذا أثرت عملي صف بسيطة E على المصفوفة المحايدة In للحصول على مصفوفة بسيطة، فإنه توجد عملية صف ثانية إذا أثرت على E ستعيدها إلى In.
مثال (3):
نفرض أن E مصفوفة ناتجة من ضرب الصف رقم i في المصفوفة In بالثابت غير الصفري k.
وإذا ضربنا الصف رقم i من المصفوفة E بالثابت 1/k فإننا سنحصل على المصفوفة In، العمليات التي تعيد E إلى In تسمى العمليات العكسية.
مبرهنة (1-2):
كل مصفوفة بسيطة قابلة للانعكاس وكذلك المعكوس مصفوفة بسيطة.
البرهان:
لتكن E مصفوفة بسيطة ناتجة عن تأثير عملية صفية بسيطة على In. أفرض أن E' مصفوفة ناتجة من تأثير معكوس هذه العملية على In، وبموجب الملاحظة أعلاه وحقيقة أن عمليات الصف العكسية تزيل تأثير أحدهما للأخرى فإن:
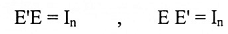
لذا فالمصفوفة البسيطة E' هي معكوس E.
مبرهنة (1-3):
لتكن A مصفوفة سعتها n x n، فإن الصيغ الآتية متكافئة، أي، إما جميعها صحيحة أو جميعاً خاطئة.
1. A قابلة للانعكاس.
2. AX = 0 لها حل وحيد هو الحل الصفري.
3. الصيغة المدرجة الصفية المختزلة للمصفوفة A هي المصفوفة In.
4. يعبر عن A كحاصل ضرب مصفوفات بسيطة.
البرهان:
1←2 : نفرض أن A قابلة للانعكاس وأن X' هو حل للنظام المتجانس AX = 0. لذا فإن AX' = 0. لذا فإن AX'= 0.
A قابلة للانعكاس فإن A-1، معكوس A، موجود . بضرب AX' = 0 بالمصفوفة A-1 من جهة اليسار نحصل على
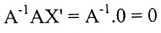
إذن X' = 0. نستنتج من ذلك أن الحل الوحيد هو الحل الصفري.
2←3 : نفرض أن AX = 0 هو الشكل المصفوفي للنظام الخطي:
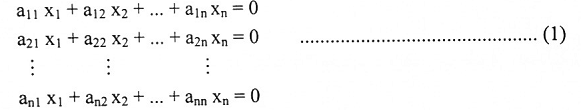
افرض أن حل هذه النظام هو الحل الصفري. إذا استخدمنا طريقة اختزال كاوس ــ جوردان فإن المعادلات المقابل للشكل المدرج الصفي المختزل للمصفوفة الممتدة سيكون:
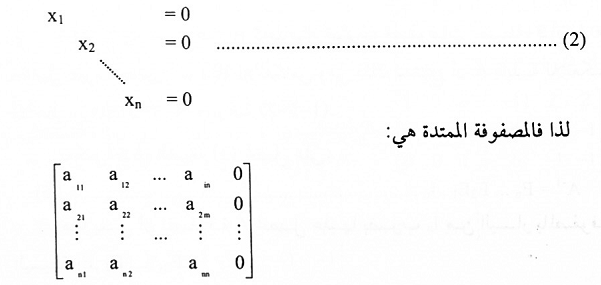
وبتطبيق عمليات الصف البسيطة على المصفوفة الممتدة للمعادلات الخطية (1) سنحصل على المصفوفة الممتدة:

وهذا يعني أن الصيغة المدرجة الصفية المختزنة للمصفوفة A هي In.
3←4 : نفرض أن الصيغة المدرجة الصفية المختزلة للمصفوفة A هو In.
نضرب A من جهة اليسار بسلسلة من عمليات الصف البسيطة فتتحول A إلى In.
3) .......................................E1E2…EnA=In
ولما كانت E1 ، E2 ، ..... ، En قابلة للانعكاس، وبضرب طرفي المعادلة (3) بالمصفوفات 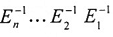 نحصل على:
نحصل على:
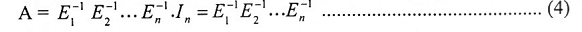
وبموجب المبرهنة (1-5-2) فإن A يعبر عنها كحاصل ضرب مصفوفات بسيطة.
4←1 : إذا عبرنا عن A كحاصل ضرب مصفوفات بسيطة، فإن A هي حاصل ضرب مصفوفات قابلة للانعكاس ومن ذلك نستنتج أن A قابلة للانعكاس [لاحظ مبرهنة (1-4-5) ومبرهنة (1-5-2).
بعكس طرفي الصيغة (3) نحصل على:
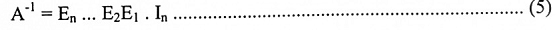
هذا يعني أن المصفوفة A نحصل عليها بضرب In من اليسار بالمصفوفات البسيطة En,….,E2,E1
وبمقارنة العلاقتين (3) و (5) يتبين لنا أن سلسلة عمليات الصف التي تحول A إلى In ستحول In إلى A-1.
طريقة إيجاد معكوس المصفوفة القابلة للانعكاس:
تتلخص هذه الطريقة بإيجاد عمليات صف بسيطة تحول A إلى In ومن ثم استخدام نفس هذه السلسلة نفس هذه السلسلة من العمليات على المصفوفة المحايدة بجوار A للحصول على A-1. وللقيام بذلك نضع المصفوفة المحايدة على يمين A للحصول على الشكل [A : In] ومن ثم إجراء عمليات الصف على هذه المصفوفة حتى يتحول الجانب الأيسر إلى In. هذه العمليات ستحول الجانب الأيمن إلى A-1، وسنحصل على الشكل [In : A-1].
مثال (4):
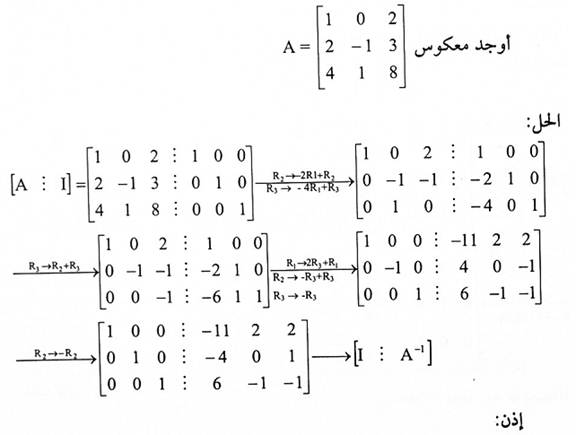
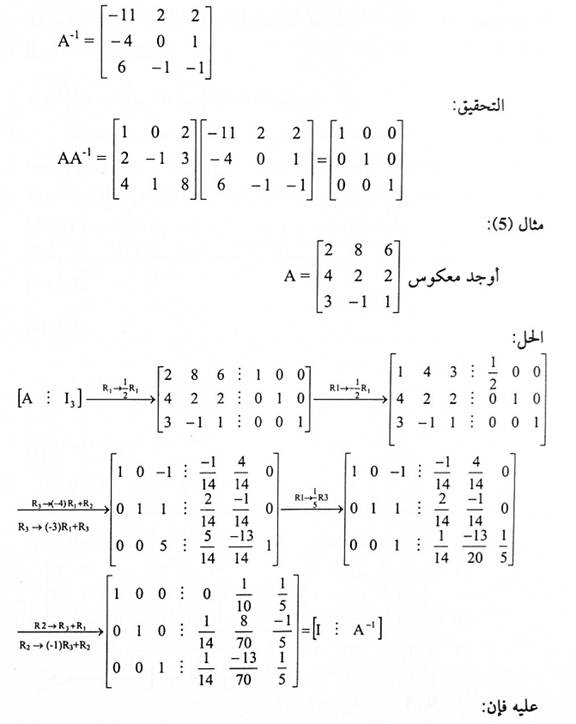
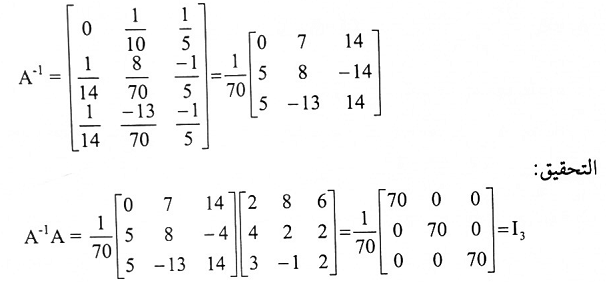
ملاحظة:
من غير الممكن مسبقاً معرفة فيما إذا كانت A مصفوفة قابلة للانعكاس أم لا. فإذا كانت A غير قابلة للانعكاس فلا يمكن اختزالها إلى In بموجب العمليات الصفية البسيطة، بمعنى آخر، أن الشكل المدرج الصفي المختزل للمصفوفة A يحتوي على الأقل على صف واحد جميع عناصره أصفار.
مثال (6):
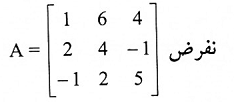
الحل:
باعتماد الطريقة الموضحة في المثالين 4 و 5 نحصل في إحدى خطوات الحل على الشكل الآتي:
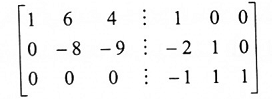
إذ أن الصف رقم 3 من المصفوفة من الجهة اليسرى جميع عناصره أصفار. لذا فالمصفوفة غير قابلة للانعكاس.
 الاكثر قراءة في الجبر الخطي
الاكثر قراءة في الجبر الخطي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















