دالة المحدد

ظهرت فكرة المحددات لأول مرة عند حل أنظمة المعادلات الخطية وللمحددات تطبيقات مهمة في العديد من مواضع الجبر الخطي كما سنرى في الفصول القادمة. في هذا البند سوف ندرس دالة المحدد، التي هو دالة القيمة الحقيقية للمتغير A,A مصفوفة. بمعنى آخر، أنها ترافق العدد الحقيقي (AF)مع المصفوفة A.

تعريف (1-1):

التبديلة لمجموعة n من الأعداد الصحيحة {1 ,2 … , n} هي ترتيب تلك الأعداد بشكل معين بدون حذف أو تكرار.

مثال (1):

توجد ست تبديلات مختلفة للمجموعة x={1,2,3} :

(1,2,3)                       (2,1,3)                       (3,1,2)

(1,2,3)                       (2,3,1)                       (3,2,1)

الطريقة الملائمة لجدولة التبديلات هي في استعمال شجرة التبديلات والتي سنيينها في المثال الآتي:

مثال(2):

اوجد جميع تبديلات المجموعة {1,2,3,4}.

الحل: نعين أربعة نقاط كل نقطة تمثل أحد أعداد المجموعة وتكون الشجرة الموضحة في الشكل (1- 1).

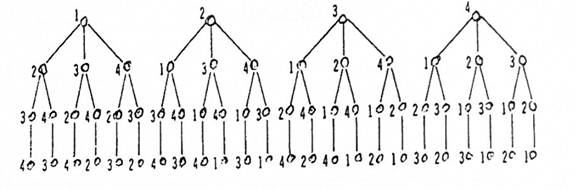
                                                      شكل (1-1)

النقاط الأربعة في أعلى الشكل تمثل الاختيارات الممكنة للعدد الأول من التبديلة . الفروع الثلاث المستقيمة من هذه النقاط تمثل الاختيارات الممكنة للموقع الثاني في التبديلة. فمثلاً إذا بدأت التبديلة (2,-,-)، أي أن التبديلة بدأت بالعدد 2، فإن الاحتمالات الثلاث للموقع الثاني هي 1 أو 3 أو 4. الفرعين المتشعبين من ل نقطة من الموقع الثاني  يمثلان الاختيارات الممكنة للموقع الثالث. فإذا بدأ التبديلية (2,3,-,-) فإن الاختيارين الممكنين للموقع الثالث هما 1 و4. وأخيراً الفرع الوحيد المتشعب في كل نقطة في الموقع الثالث يمثل الاختيار الوحيد للموقع الرابع. فإذا بدأت التبديلية مع (2,3,4,-) فإن الاختيار الوحيد للموقع الرابع هو 1.

التبديلات المختلفة يمكن جدولتها من خلال رسم جميع احتمالات ممرات الشجرة بدء من الموقع الأول والغاية الموقع الرابع. لاحظ الجدول الآتي:

من خلال المثال أعلاه وجدنا أن عدد تبديلات المجموعة (1,2,3,4) هو 24. يمكن الحصول على هذه العدد بطريقة ثانية بدون جدولة التبديلات. بما أن هناك احتمالات لإشغال الموقع الأول فإن الموقع الثاني يمكن إشغاله بثلاث الموقع الثالث سيشغل بطريقتين فإننا نحصل على 4,3,2 طريقة لاشغال المواقع الثلاثة الأولى، وأخيراً، لما كان الموقع الأخير سيشغل بطريقة واحدة فقط، فإننا سنحصل على 4.3.2.1 = 24 طريقة لاشغال المواقع الأربعة.

بصورة عامة المجموعة {1,2,…,n} تمتلك n! = n (n-1) .. 2.1

تبديلة مختلفة (n! يسمى مضروب n).

التعاكسات:

نرمز للتبديلة العامة للمجموعة {1,2,…,n} بالرمز (j₁ , j₂, … , j_n) حيث j₁ يمثل العدد الأول في التبديلة ، j₂ يمثل العددح الثاني وهكذا.

نقول أن التبديلة (j₁ , j₂, … , j_n) تحتوي على تعاكس عندما يوجد عدد كبير يسبقه عدداً أصغر، وعدد التعاكسات في التبديلة يمكن إيجاده بالطريقة الآتية:

1. نحسب عدد الأعداد التي هي أصغر من j₁ وتأتي قبله.

2. نحسب عدد الأعداد التي هي أصغر من j₂ وتأتي قبله.

3. نستمر في طريقة الحساب هذه بالنسبة للأعداد j₄, j₃ إلى j_n-1.

4. مجموعة الأعداد التي نحصل عليها يمثل عدد التعاكسات في التبديلة.

مثال (3):

احسب عدد التعاكسات في التبديلات التالية:

(1,2,3,4) .C  (2,4,1,3)  .b(5,3,2,4)  .a

الحل: 

a. 1. عدد الأعداد التي هي أصغر من 5 وتأتي قبلها هي 3.

2. عدد الأعداد التي هي أصغر من 3 وتأتي قبلها هي 1.

3. عدد الأعداد التي هي أصغر من 2 وتأتي قبلها هي صفر.

          . . مجموعا الأعداد في 1 ، 2 ،3 هو 3+1 + 0 = 4

باعتماد الطريقة في (a) نفسها، نحصل على:

b. مجموع التعاكسات 3.

c. مجموع التعاكسات صفر.

تعريف (1-2):

يقال للتبديلة بأنها زوجية إذا كان المجموع الكلي للتعاكسات فيها عدد زوجي وتسمى فردية إذا كان المجموع الكلي للتعاكسات عدد فردي.

مثال (4):

احسب عدد التعاكسات والتبديلات الزوجية والفردية لما يلي:

(1,4,3,2) , (4,3,2,1) , (3,4,2,1) , (2,3,1,4) , (1,2,4,3)

الحل:

تعريف (1-3):

الضرب البسيط من المصفوفة A التي سعتها n × n هو ضرب n من عناصر A بحيث لا يتكرر عنصرين منها من نفس الصف أو العمود.

مثال (5):

اوجد جميع حواصل الضرب البسيط للمصفوفة:

الحل:

بما أن حاصل الضرب البسيط للمصفوفة A يتكون من ثلاث عوامل كل منها يأتي من صف مختلف، فإن حاصل الضرب البسيط يمكن كتابته بالشكل:

                                                                   a₁-a₂-a₃-

وبما أن حاصل الضرب لا يحتوي على عاملين متكريين من نفس العمود فإن الأعداد التي تمثل رقم العمود لا تتكرر وعليه فإنها يجب أن تكون من تبديلات المجموعة {1,2,3}. التبديلات الستة هذه تعطينا خواص الضرب البسيطة الآتية:

من الشكل أعلاه نستطيع أن نقول ان المصفوفة A ذات السعة n×n تحتوي على n! من حواصل الضرب البسيط ويمكن تمثيلها بالشكل:

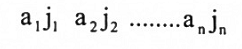
حيث ...(j₁,j₂,…, j_n) تبديلة للمجموعة {1,2,…, n}.

حاصل الضرب البسيط من A ذي الإشارة نعني به حاصل الضرب a₁j₁ a₂j₂ ………a_n j_n مضروباً بالإشارة + او - . نستعمل + إذا كانت التبديلة (j₁,j₂,…,j_n) زوجية و – للتبديلة الفردية.

أوجد جميع حواصل الضرب البسيط ذي الإشارة للمصفوفة:

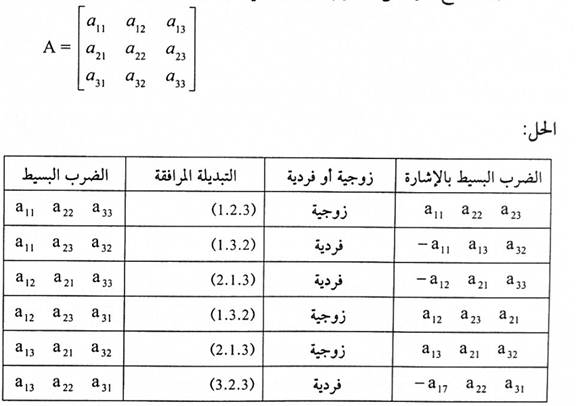
تعريف (1-4):

لتكن A مصفوفة مربعة، فإن دالة المحدد، تكتب Adet، تعرف بأنها مجموع جميع حواصل الضرب البسيط ذي الإشارة من A. الرمز A det يسمى محدد A، محدد A يكتب للسهولة بالشكل |A|.

طريقة حساب محدد المصفوفات ذات السعة 2 x 3 و 3 x 3

مثال(7):

اوجد محدد كل من المصفوفات الآتية:

من الصعوبة أحياناً حفظ الحدود الجبرية أعلاه ولذا نقترح اعتماد الطريقة الآتية:

a. الصيغة الاولى من المثال 7 نحصل عليها من          ضرب العناصر الواقعة على السهم المتجه من اليسار إلى اليمين مطروحاً منها ضرب  العناصر الواقعة على السهم المتجه من اليمين إلى اليسار، لاحظ الشكل (1-2)a.

b. اما الصيغة الثانية فنحصل عليها كما يلي:

1. نكتب المصفوفة ذات السعة n x n نضع بجوارها من جهة اليمين العمودين الأول والثاني لنفس المصفوفة.

2. تحسب المحدد بجميع حاصل ضرب العناصر الواقعة على الأسهم المتجه من اليسار إلى اليمين مطروحاً منها حواصل ضرب العناصر على الأسهم المتجه من اليمين إلى اليسار لاحظ الشكل (1-2)b.

                                                          شكل (1-2)

مثال (8):

اوجد محدد كل من المصفوفات الآتية:

تنبيه:

الصيغ الموضحة في الشكل (1-2)  تصلح فقط للمصفوفات ذات السعة 2 x 2 و 2 x 3 ولا تصلح للمصفوفات ذات السعة 4 x 4  صعوداً.

واخيراً يمكن إيجاد محدد أي مصفوفة A ذات السعة n x n بالصيغة:

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تشارك بأكثر من 750 إصدارًا في معرض بغداد الدولي للكتاب

تيمنًا بذكرى ولادة الصادقَين (صلوات الله عليهما) شعبة التوجيه النسوي تنظم مسابقة ميدانية لزائرات مرقد أبي الفضل العباس (عليه السلام)

المجمع العلمي ينظّم أنشطةً قرآنية في محافظتي كربلاء والديوانية

العتبة العباسية المقدسة تختتم فعاليات مهرجان رحمة للعالمين الدولي الأوَّل

المزيد

الآخبار الصحية

تحذير من الإفراط في شربها.. متى تصبح الماتشا خطيرة؟

من بناء العضلات إلى "تسميم الجسم".. الوجه الآخر للبروتين ؟

دراسة جديدة: مخ الانسان يغتسل أثناء النوم

هل من الآمن شرب القهوة على معدة فارغة؟

المزيد

الآخبار التكنلوجية

مزايا مرآة الرؤية الخلفية ذاتية التعتيم في السيارات

دراسة.. كوكب غريب أمد الأرض بمقومات الحياة !

يهدد عرش هوليود.. أول فيلم رسوم متحركة بالذكاء الاصطناعي

أكبر تغيير منذ سنوات.. هل تكشف أبل النقاب عن "iPhone Air"؟

المزيد

مواضيع ذات صلة

فضاء المتجهات الإقليدي-تمارين محلولة

فضاء المتجهات الإقليدي-تمارين محلولة

فضاء المتجهات الإقليدي-الفضاء الاقليدي النوني

فضاء المتجهات العام- فضاء المتجهات الحقيقي

فضاء المتجهات العام-رتبة المصفوفات بعد الفضاء الصفري

فضاء المتجهات العام-فضاء الصفوف وفضاء الأعمدة والفضاء الصفري

فضاء المتجهات العام- الأساس والبعد

فضاء المتجهات العام-الفضاءات الجزئية

فضاء الضرب الداخلي-الأساسات المتعامدة طريقة كرام ــ شمت

فضاء الضرب الداخلي-الضرب الداخلي

فضاء الضرب الداخلي-المصفوفات المتعامدة، تبديل الأساسات

فضاء الضرب الداخلي-الزوايا والتعامد في فضاء الضرب الداخلي