التساؤل الثاني هو أي مصفوفة يمكن أقطرتها تعامدياً وكيفية إيجاد مصفية متعامدة يمكن استخدامها في الأقطرة.

مبرهنة (1-1): إذا كانت A مصفوفة سعتها n x n فإن التعابير الآتية متكافئة:

1. A قابلة للأقطرة تعامديا.

2 A. تحتوي على مجموعة n من المتجهات الذاتية العيارية المتعامدة.

3. A مصفوفة متناظرة (أي A^T = A).

البرهان:

1←2: لما كانت A قابلة للأقطرة التعامدية فإنه توجد مصفوفة متعامدة مثل P بحيث P^-1AP قطرية. عليه فإن متجهات أعمدة P التي عددها n هي المتجهات الذاتية للمصفوفة A. لذا فإن A تحتوي على n من المتجهات الذاتية العيارية المتعامدة.

2←1: لتكن {v₁, v₂, …… , v_n} هي المتجهات الذاتية العيارية المتعامدة التي عددها n. بموجب برهان المبرهنة (1-2)في(اقطرة المصفوفة) فإن المصفوفة P التي أعمدتها هي

المتجهات الذاتية هذه تؤقطر A. وبما أن هذه المتجهات هي عيارية، لذا فإن P متعامدة ولذلك فهي تؤقطر A تعامديا.

1←3: لاحظنا من 1←2 إن المصفوفة A ذات السعة n x n القابلة للأقطرة تعامديا مؤقطرة تعامديا بواسطة المصفوفة P ذات السعة n x n والتي أعمدتها تؤلف مجموعة عيارية متعامدة من متجهات A الذاتية.

نفرض P^-1AP = D حيث D مصفوفة قطرية. لذا:

إذن A متناظرة.

خواص المصفوفة المتناظرة:

نفرض A مصفوفة متناظرة.

1. المتجهات الذاتية للمصفوفة A جميعها أعداد حقيقية.

2. المتجهات الذاتية المأخوذة من فضاءات ذاتية مختلفة تكون متعامدة.

طريقة أقطرة المصفوفة المتناظرة عمودياً

1. نجد أساس كل فضاء ذاتي لــ A.

2. استخدام طريقة كرام ــ سمث لكل من هذه الأساسات لإيجاد الأساس العياري المتعامد لكل فضاء ذاتي.

3. كون P التي أعمدتها متجهات الاساس الناتج من الفقرة (2)

4. المصفوفة P هذه تؤقطر A تعامديا.

مثال(1):

أوجد المصفوفة المتعامدة التي تؤقطر المصفوفة

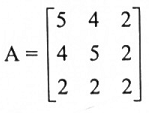
الحل:

بما أن A متناظرة فإن معادلتها المميزة هي:

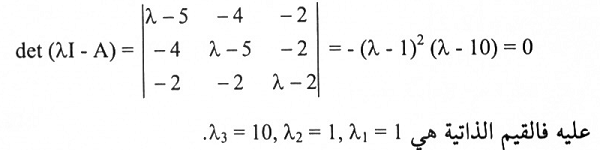
باعتماد طريقة إيجاد المتجهات الذاتية الواردة في البند (القيم الذاتية والمتجهات الذاتية) نحصل على:

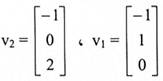.وهي المتجهات الذاتية المرافقة لــ1= λ

كذلك هي أساس الفضاء الذاتي المرافق لــ1=λ

كما وأن:

 هو المتجه الذاتي لمرافق لــ 10=λ

نوجد P باستخدام طريقة كرام ــ سمث على {v₁, v₂}.

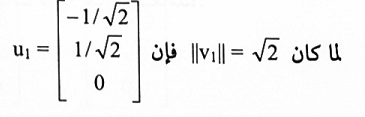
وأخيراً نستخدم طريقة كرام ــ سمث على أساس الفضاء الذاتي {v₃}.

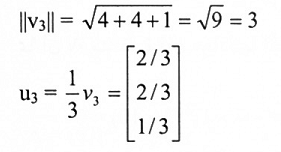
ملاحظة:

حقق صحة الحل.

لاحظ أن u₃,u₂,u₁ هي متجهات ذاتية عيارية متعامدة.

مثال(2):

أوجد المصفوفة المتعامدة التي تؤقطر                                                               .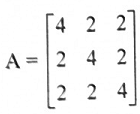

الحل:

وإذا أخذنا u₃,u₂,u₁ كمتجهات أعمدة فنحصل على:

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

فضاء المتجهات الإقليدي-تمارين محلولة

فضاء المتجهات الإقليدي-تمارين محلولة

فضاء المتجهات الإقليدي-الفضاء الاقليدي النوني

فضاء المتجهات العام- فضاء المتجهات الحقيقي

فضاء المتجهات العام-رتبة المصفوفات بعد الفضاء الصفري

فضاء المتجهات العام-فضاء الصفوف وفضاء الأعمدة والفضاء الصفري

فضاء المتجهات العام- الأساس والبعد

فضاء المتجهات العام-الفضاءات الجزئية

فضاء الضرب الداخلي-الأساسات المتعامدة طريقة كرام ــ شمت

فضاء الضرب الداخلي-الضرب الداخلي

فضاء الضرب الداخلي-المصفوفات المتعامدة، تبديل الأساسات

فضاء الضرب الداخلي-الزوايا والتعامد في فضاء الضرب الداخلي