


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 3-10-2020
التاريخ: 18-10-2021
التاريخ: 18-11-2021
التاريخ: 15-9-2016
|
التماثل الكروي
من امثلة التماثل الكروي، الشحنات النقطية، والشحنات الموزعة بانتظام فوق الأسطح أو الحجوم الكروية. ولنعتبر شحنة كلية مقدارها +Q منتشرة بانتظام فوق كرة مفرغة وخلوية ونصف قطرها R كما في الشكل (1 أ). وعند أية نقطة ولتكن A خارج الكرة فإننا نستطيع استخدام اعتبارات التماثل لإثبات أن كل المركبات المستعرضة (أي المركبات العمودية على الاتجاه القطري) للقوة والمؤثرة على شجنة اختبار ومن ثم اتجاه المجال E تتجه قطرياً نحو الخارج انطلاقاً من مركز الكرة. كما تتيح لنا اعتبارات التماثل أن نقول بأن كل النقط الواقعة عند نفس المسافة r من المركز تكون متكافئة. وإذا اخترنا السطح الجاوسي على هيئة كرة (ذات اللون الأخضر). نصف قطرها r ( يمر خلال A) ، فإننا نستطيع أن نضع النصوص التالية:
1ـ للمجال E نفس المقدار عند كل النقط الواقعة على السطح الجاوسي، حتى وإن كنا لا نعرف ما هو ذلك المقدار بعد.
2- E عمودي على السطح الجاوسي عند كل النقط ولذا فهو يتجه قطرياً نحو الخارج انطلاقاً من مركز الكرة.
وتمكننا هذه المعلومات من حساب الطرف الأيسر من قانون جاوس :
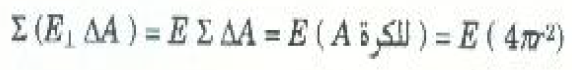
أما المقدار الذي بالطرف الأيمن لقانون جاوس فهو مجرد الشحنة الإجمالية فوق الكرة المجوعة أو Q. وهكذا فإن قانون جاوس يؤدي إلى الحل الخاص بالمقدار E:
(1أ) 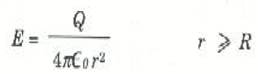
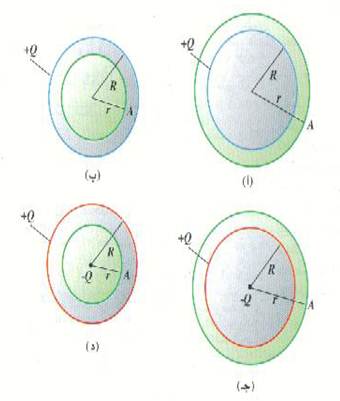
الشكل (1)
وهذا يوضح أنه، بالنسبة للنقط التي إما على التوزيع الكروي للشحنات أو خارجه فإن المجال الكهربي سيكون نفس المجال الذي ينشأ كما لو كانت الشحنات كلها عند مركز الكرة. فإذا كانت الشحنة على الكرة هي -Q فسنحصل على نفس النتيجة باستثناء أن اتجاه E سيكون قطرياً إلى الداخل.
دعنا الآن نختار سطحاً جاوسياً داخل الكرة المجوفة (r < R) كما في الشكل (1 ب). إن نفس اعتبارات التماثل لازالت قائمة والطرف الأيسر من قانون جاوس هو أيضاً (4πr2) E. ولكن بما أننا نعتبر الكرة خاوية ، فإن السطح لا يحتوي بداخله على أية شحنات ولذا يصبح قانون جاوس كالتالي:
(1 ب) 
بما يعني أن : E = 0
عند كل النقاط داخل الكرة المشحونة المجوفة.
أما في الشكل (1 جـ ، د )، فقد قمنا بوضع شحنة نقطية – Q في مركز نفس الكرة المشحونة، ويحتفظ هذا الوضع بالتماثل الكروي السابق بأكمله. وإذا اعتبرنا نفس السطح الجاوسي كما سبق لوجدنا أن السطح الخارجي لا يحيط بأية شحنة صافية، بينما يحيط السطح الداخلي بشحنة صافية مقدارها – Q. ويمكننا على الفور استنتاج أن المجال الناشئ عن توزيع الشحنات في الشكل (1 جـ و د) هو:
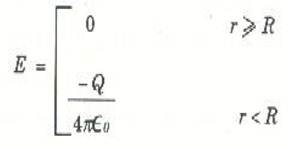



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|