Albert Einstein

Like Columbus

Modern theoretical physicists like to think of themselves as intellectual explorers, and the greatest of them have indeed discovered new and exotic physical worlds, both microscopic and macroscopic. Travel in these intellectually distant realms has proved hazardous because it takes the explorer far from the world of ordinary experience. Werner Heisenberg, one of the generation of theorists who found the way to the quantum realm, the strangest of all the physical worlds, likened the intellectual expeditions of modern physics to the voyage of Columbus. Heisenberg found Columbus's feat remarkable not because Columbus tried to reach the East by sailing west, nor because he handled his ships masterfully, but because he decided to “leave the known regions of the world and sail westward, far beyond the point from which his provisions could have got him back home again.” The man who ranks above all others as an intellectual Columbus is Albert Einstein. He took such expeditions far beyond “the safe anchorage of established doctrine” into treacherous, uncharted seas. Not only was he a pioneer in the quantum realm; he discovered and explored much of the territory of modern physics.

These great explorations were started, and to a large extent completed, when Einstein was in his twenties and working in a quiet corner of the scientific world, the Swiss Patent Office in Bern. Life in the patent office, as Einstein found it, was a “kind of salvation.” The work was interesting, and not demanding; without the pressures of an academic job, he was free to exploit his marvelous ability “to scent out that which was able to lead to fundamentals and to turn aside from everything else, from the multitude of things which clutter up the mind and divert it from the essential.”

Einstein had tried to place himself higher professionally, but his prospects after graduating from the Zurich Polytechnic Institute (since 1911 known as the Swiss Technical University or ETH) were not brilliant. He had disliked and opposed most of his formal education. The teachers in his Munich gymnasium said he would never amount to anything, and deplored his disrespectful attitude. The gymnasium experience aroused in Einstein a profound distrust of authority, particularly the kind wielded by Prussian educators. Ronald Clark, one of Einstein's biographers, describes the Luitpold Gymnasium Einstein attended in Munich as probably “no better and no worse than most establishments of its kind: It is true that it put as great a premium on a thick skin as any British public school but there is no reason to suppose that it was particularly ogreish. Behind what might be regarded as not more than normal discipline it held, in reserve, the ultimate weapon of appeal to the unquestionable Prussian god of authority. Yet boys, and even sensitive boys, have survived as         much.”

Einstein's father, Hermann, was a cheerful optimist “exceedingly friendly, mild and wise,” as Einstein recalled him but prone to business failures. One of these drove the family from Munich to Milan, with Einstein left behind to complete his gymnasium courses. He had few friends among his classmates, and now with his family gone, he could no longer bear life in Munich, or anywhere else in Germany. He abruptly joined his family members in Italy and informed them that he planned to surrender his German citizenship. That meant no gymnasium diploma, but Einstein planned to do the necessary studying himself to prepare for the Zurich Poly entrance examination. Life in Italy, and later in Switzerland, was free and promising again, and it “transformed the quiet boy into a communicative young man,” writes Abraham Pais, a recent Einstein biographer. For a few happy months, Einstein celebrated his release from a dismal future by roaming northern Italy.

A temporary setback, failing marks in the Poly admission examination, proved to be a blessing. To prepare for a second try, Einstein attended a Swiss cantonal school in Aarau, where the educational process was, for a change, a joy. In Aarau, Einstein lived with the Winteler family. Jost Winteler was the head of the school, and “a somewhat casual teacher,” writes Clark, “as ready to discuss work or politics with his pupils as his fellow teachers. [He] was friendly and liberal minded, an ornithologist never happier than when he was taking his students and his own children for walks in the nearby mountains.” Even in old age, Einstein recalled vividly his year in Aarau: “This school left an indelible impression on me because of its liberal spirit and the unaffected thoughtfulness of the teachers, who in no way relied on external authority.”

In early 1896, Einstein paid a fee of three marks and was issued a document declaring that he was no longer a German citizen; he would be a stateless person for the next five years. Later in the year he passed the Zurich Poly examination with good marks and began the four-year preparation of a fachlehrer, a specialized high-school teacher. Hermann had suffered another business disaster, so Einstein's means were now limited a monthly allowance of one hundred Swiss francs, from which he saved twenty francs to pay for his Swiss naturalization papers. But there was nothing meager about his vision of the future. In a letter to Frau Winteler, he wrote, “Strenuous labor and the contemplation of God's nature are the angels which, reconciling, fortifying and yet ceaselessly severe, will guide me through the tumult of life.”

On the whole, Einstein did not respond with much enthusiasm to his course work at the Zurich Poly. He recognized that some of the mathematics courses were excellent one of his mathematics professors, Hermann Minkowski, later made vital contributions to the mathematical foundations of the theory of relativity but the courses in experimental and theoretical physics were uninspiring. At first he was fascinated by laboratory work, but his experimental projects rarely met with the approval of his professor, Heinrich Weber. In exasperation, Weber finally told his pupil, “You are a smart boy, Einstein, a very smart boy. But you have one great fault: you do not let yourself be told anything.”

Einstein responded by simply staying away from classes and reading in his rooms the great nineteenth-century theorists, Kirchhoff, Helmholtz, Hertz, Maxwell, Hendrik Lorentz, and Boltzmann. Fortunately, the liberal Zurich program allowed such independence. “In all there were only two examinations,” Einstein writes in his autobiographical notes, “aside from these, one could just about do as one pleased. . . . This gave one freedom in the choice of pursuits until a few months before the examination, a freedom which I enjoyed and have gladly taken into the bargain the bad conscience connected with it as by far the lesser evil.”

The punishment appears to have been more than a bad conscience, however. Preparation for the final examination was a nightmare, and the outcome successful largely due to the help of a friend, Marcel Grossmann, who had a talent for taking impeccable lecture notes. Einstein tells us, again in his autobiographical notes, that the pressure of that examination “had such a deterring effect [on me] that, after I had passed . . . I found consideration of any scientific problems distasteful for an entire year.” And he adds this thought concerning the heavy hand the educational system lays on a student's developing intellectual interests: “It is, in fact, nothing short of a miracle that the modern methods of instruction have not yet entirely strangled the holy curiosity of inquiry; for this delicate little plant, aside from stimulation, stands mainly in need of freedom.”

Einstein graduated from the Poly in the fall of 1900, and a few months later passed two important milestones in his life: he published his first paper in volume 4 of the Annalen der Physik, which contained, just forty pages later, Max Planck's inaugural paper on quantum theory and he received his long-awaited Swiss citizenship. Although he was to leave Switzerland nine years later, and did not return to settle, Einstein never lost his affection for the humane, democratic Swiss and their splendid country, “the most beautiful corner on Earth I know.”

He was now job hunting. An expected assistantship at the Zurich Poly under Weber never materialized. (“Weber . . . played a dishonest game with me,” Einstein wrote to a friend.) Two temporary teaching positions followed, and then with the help of Marcel Grossmann's father, Einstein was appointed technical expert third class at the Bern Patent Office in 1902.

Now that he had steady employment, Einstein thought of marriage, and a year later he and Mileva Maric, a classmate at the Zurich Poly, were married. Mileva came from a Slavic-Serbian background. She was pretty, tiny in stature, and slightly crippled from tuberculosis in childhood. She had hoped to follow a career in science, and went to Zurich because Switzerland was the only German speaking country at the time admitting women to university studies. The couple became lovers soon after both entered the program at the Zurich Poly. By 1901, the affair had deepened: Mileva was pregnant. In 1902, a daughter, Liserl, was born at Mileva's parents’ home in Novi Sad. When she returned to Zurich, Mileva did not bring the baby, and in 1903, shortly after Einstein and Mileva were married, the girl was apparently given up for adoption.

The marriage was never a success. After the trials of her pregnancy, a difficult birth, and the loss of the child, Mileva's career plans collapsed. She was jealous of Einstein's freewheeling friends, and prone to periods of depression. On his side, Einstein was not a sensitive husband; too much of his intellectual and emotional strength was spent on his work to make a difficult marriage succeed. In old age, Einstein recalled that he had entered the marriage with a “sense of duty.” He had, he said, “with an inner resistance, embarked on something that simply exceeded my strength.”

Doctrine of Space and Time

For Einstein, there were two important kinds of theories. “Most of them are constructive,” he wrote. “They attempt to build up a picture of the more complex phenomena out of the materials of a relatively simple formal scheme from which they start out.” As an example, he cited the molecular theory of gases. It begins with the hypothesis of molecular motion, and builds from that to account for a wide variety of mechanical, thermal, and diffusional properties of gases. “When we say that we have succeeded in understanding a group of natural processes,” Einstein continued, “we invariably mean that a constructive theory has been found which covers the processes in question.”

Theorists since Galileo and Newton have also created what Einstein called “principle theories.” These are theories that “employ the analytic, not the synthetic, method. The elements which form their basis and starting point are not hypothetically constructed but empirically discovered ones, general characteristics of natural processes, principles that give rise to mathematically formulated criteria which the separate processes or the theoretical representations of them have to satisfy.” The supreme example of a principle theory, Einstein pointed out, is thermodynamics, based on the energy and entropy principles called the first and second laws of thermodynamics.

Einstein saw relativity as a principle theory. He began his 1905 paper on relativity by postulating two empirical principles on which his theory, with all its startling conclusions, would rest. The first principle generalized Galileo's relativity principle by asserting that (as Einstein put it several years later),

The laws of nature are independent of the state of motion of the frame of reference, as long as the latter is acceleration free [that is, inertial].

The phrase “laws of nature” is all-inclusive; it encompasses the laws of electromagnetic and optical, as well as mechanical, origin. This is a grandly democratic principle: all inertial frames of reference are equal; none is different or preferred.

The second of Einstein's principles gives formal recognition to the constancy of the speed of light:

Light in empty space always propagates with a definite [speed], independent of the state of motion of the emitting body.

Whereas Lorentz had struggled to explain the invariance of the speed of light with a constructive theory that hypothesized motion-dependent molecular forces, Einstein bypassed all the complications by simply promoting the constancy to a postulate. For Lorentz and his contemporaries, it was a problem, for Einstein a principle.

Einstein's two principles led him to conclude that the speed of light in free space is the only measure of space and time that is reliably constant from one observer to another. All else is relative. Different observers cannot express their physical laws in a shared, absolute frame of reference, as Newton taught. Observers in different inertial frames find that their physical worlds are different according to a new “doctrine of space and time,” as Einstein put it.

We can follow the rudiments of Einstein's argument by first considering the elementary question of time measurements. Imagine a timing device recommended by Einstein, called a “light clock”; figure 1.1 displays the light clock as it is seen by an observer who travels along with it. Light flashes are generated by the source S; they travel to the mirror M, and are reflected back to the detector D. The short time for one flash to make the round trip from S to M to D represents one “tick” of the clock. If c is the speed of light, and L₀ is the distance from S and D to M, this time, call it Δt₀, is equal to L₀/c for the trip from S to M, and also for the return trip from M to D, so

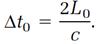 (1)

Now, keeping in mind Einstein's principle of the constancy of the speed of light, we look at the light clock from the point of view of a second observer, who sees the clock in an inertial frame moving at the constant speed v. Figure 1.2 shows the path of a light flash as seen by this observer. The clock is shown in

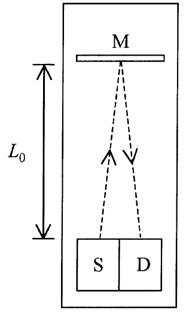
Figure 1.1. Einstein’s light clock, as seen by an observer traveling with the clock. The distance between the source and the detector is exaggerated. This figure, the one that follows, and fig.1.4 are adapted with permission from Robert Resnick, David Halliday, and Kenneth Krane, Physics, 4th ed.(New York: Wiley, 1992), 470.

three positions: at A when the light flash leaves the source, at B when it is reflected by the mirror, and at C when it reaches the detector. (The inertial frame containing the light clock is moving extremely fast: Galileo's ship has become a spaceship.) The time representing one tick of the clock is now Δt, and the clock moves the distance vΔt in that time. The corresponding distance traveled by the light flash is 2L, and that is clearly greater than the distance 2L₀ the light flash travels for the first observer during one tick of the clock. The speed of light is exactly the same for both observers, Einstein's principle insists, so the time Δt for one tick according the second observer is greater than the time Δt₀ for one tick according to the first observer. In other words, the two observers perceive the clock ticking at different rates; it goes slower for the observer who sees the clock moving.

The mathematical connection between Δt and Δt0 follows from the geometry of figure 1.2. The time interval for the light to travel the distance is 2L is

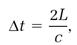 (2)

and as shown in the diagram in figure 1.3, abstracted from figure 1.2,

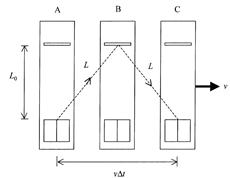
Figure 1.2. Einstein’s light clock as seen by an observer who observes the clock moving at constant speed v.

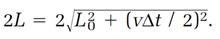
Therefore,

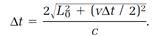
Substituting for L₀ from equation (1) and solving for Δt, we arrive at

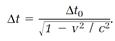   (3)

If the speed v has any ordinary value, that is, much less than the speed of light c, the ratio v/c is very small, the denominator in equation (3) is nearly equal to one,  Δt = Δt₀, and time measurements are not appreciably affected. As v approaches c, however, the denominator becomes less than one, Δt is greater than Δt₀ and time measurements are different for the two observers.

Equation (3) places limitations on the speed v: with v = c the equation generates a physically questionable infinite value for Δt, and with v > c the square root becomes an “imaginary” number in mathematical parlance, and even more unacceptable physically. We will find this prohibition on any speed equal to or larger than the speed of light to be a general feature of Einstein's theory.

The relativistic calculation of time intervals expressed by equation (3) speaks of real physical effects, not just artifacts of the mathematics. Light clocks, and all other physical aspects of time, including aging, are really seen differently by different observers moving (at high speed) relative to each other. In fact, if we can boost ourselves to a speed comparable to c relative to Earth which is possible and not dangerous if we accelerate to the high speed slowly, as in a spaceship accelerating at the rate of Earth’s gravitational acceleration g we can enter a time machine and age decades while Earth and its inhabitants age millennia.

In company with this slowing or dilation of time in a moving inertial frame, Einstein's principles also demand a contraction of length measurements. This, too, can be demonstrated with the handy light clock. As in figure 1.2, we see the clock moving at a constant speed v, but this time parallel to its length, as shown in figure 1.4.

We again imagine that a light flash is produced by the source S, and that the flash is reflected by the mirror M back to the detector D. Let Δt₁ be the time interval for the light to travel from the source to the mirror. During this time, the mirror moves through the distance vΔt₁, so the light flash must travel L + vΔt₁ to

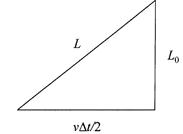
Figure 1.3. A right triangle constructed from the distances shown in fig.1.2, demonstrating that according to the Pythagorean theorem L2 = L² ₀ + (vΔt / 2)² or L =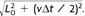 

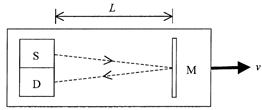
Figure 1.4. Einstein’s light clock again, as perceived by an observer who sees the clock moving parallel to the clock’s length at constant speed v.

reach the mirror. Noting that the speed of light is c, as always, we can calculate this same distance as cΔt₁, and write the equation

or

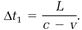 (4)

Now follow the light flash on its return from the mirror to the detector, supposing that this trip requires the time interval Δt₂. The light begins at the mirror, located at L + vΔt₁, and finishes at the detector, which has traveled the distance vΔt₂ in the first interval and vΔt₂ in the second. Thus the distance traveled by the light on its backward return trip is

The light still has the speed c, so we can also calculate this distance as cΔt₂ and obtain

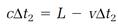
or

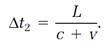
The total time interval Δt, the time for one click of the clock, is the sum of Δt₁ and Δt₂, calculated in equations (4) and (5),

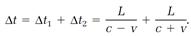
Two algebraic maneuvers (forming a common denominator and then dividing numerator and denominator by c²) convert this to

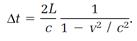 (6)

This equation reveals the length contraction when it is compared with equation (3) combined with equation (1),

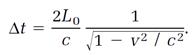
If the two calculations of Δt are compatible, we must have

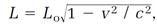 (7)

which tells us that the length Lo found by an observer traveling with the clock is contracted to 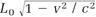for an observer watching the clock move at the constant speed v. This is the same equation that Lorentz had concluded earlier was necessary to account for Michelson and Morley's frustrated attempts to detect Earth's motion through the ether.

Equations (3) and (7), expressing the relativity of time and length, embody Einstein's new doctrine of space and time. They cover what physicists call “kinematics” that is, physics without the energy concept. Einstein's next step was to broaden his theory into a “dynamics,” with energy included. He began to construct the dynamics in another brilliant 1905 paper, where he reached “a very interesting conclusion”: “The mass of a body is a measure of its energy content.” He thought about this proposition for several years. In 1906, it occurred to him that “the conservation of mass is a special case of the law of conservation of energy.” A year later he concluded that, “With respect to inertia, mass m is equivalent to energy content of magnitude mc².” This is a verbal statement of the equation that is now the world’s most famous: E = mc².

Underlying this energy equation is the concept that mass, like time and length, is relative. Both time and length depend on the relative speed of the object observed, and so does mass. The relevant equation, which calculates the mass m of an object moving at the constant speed v, is (with no proof this time)

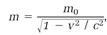 (8)  

resembling equation (3) for time intervals. At rest (v = 0), the object has its lowest mass m₀; in motion, the mass of the object increases, but only slightly at ordinary speeds much less than c.

Equation (8) equips us with some clues concerning Einstein's celebrated mc². Multiplied by c² the equation calculates mc²,

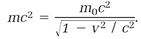 (9)

In the physics of the familiar world, v/c in this equation is very small, v² / c² is even smaller, and we can take advantage of the mathematical fact that

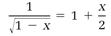
if x is very small. We apply this approximation to equation (9) with x = v² / c², and arrive at

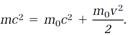
Recognizing with Einstein that E = mc², we have

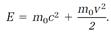 (10)

This divides the total energy E into two parts. One term, m₀ v²/2, is the familiar kinetic energy carried by an object of mass m₀. The second term, m₀c², unlocks the secret. Einstein understood this quantity, as we do today, to be a kind of potential energy possibly obtainable from the “rest mass” m₀. Because c² has an immense magnitude, this mass-equivalent energy is also immense. From a mass of one kilogram (2.2 pounds), complete conversion of mass to energy would generate energy equivalent to the daily oil consumption per day in the entire United States (fifteen million barrels). Ordinary chemical reactions convert mass to energy, but on a minuscule scale; formation of one kilogram of H₂O in the reaction

                     2 H₂ + O₂ → 2 H₂O

converts about 1.5 × 10^-10 kilogram of mass to energy. Nuclear reactions are more efficient; they convert a few tenths of a percent of the mass entering the reaction to energy. When matter meets antimatter, the conversion is complete. In his 1905 paper, Einstein suggested that radioactive materials such as radium might lose measurable amounts of mass as they decay, but for many years he could see no practical consequences of the mass-energy equivalence. (In 1934, the Pittsburgh Gazette headlined a story reporting an Einstein lecture with “Atom Energy Hope Is Spiked by Einstein. Efforts at Loosing Vast Force [Are] Called Fruitless.”) The full lesson of E = mc² was learned in the 1940s and 1950s with the advent of nuclear physics, nuclear weapons, nuclear reactors, and nuclear anxiety.

A further accomplishment of Einstein's relativity theory was that it brought a permanent end to the ether concept by simply depriving the ether of any good reason to exist. If there were an ether, it would provide an absolute and preferred frame of reference, contrary to Einstein’s first principle, and motion through the ether would be manifested by variations in the speed of light, contradicting the second principle. An ether obituary was written by Einstein and Leopold Infeld in their estimable book for the lay reader, The Evolution of Physics: “It [the ether] revealed neither its mechanical construction nor absolute motion. Nothing remained of all its properties except that for which it was invented, i.e., its ability to transmit electromagnetic waves.”

Spacetime

The new doctrine of space and time brought by Einstein's 1905 special theory demanded relativity of time as well as relativity of length and space. If an observer in an inertial frame describes some event with the coordinates x, y, z, and the time t, another observer in a different inertial frame uses different coordinates, call them x', y', z', and a different time t', to express the physics of the event. The time variable is not separate from the spatial variables, as it is in Newtonian physics. It enters the Einstein picture seemingly on the same footing as the spatial variables. This point of view was taken by one of Einstein's former mathematics professors, Hermann Minkowski, and developed into a mathematical structure that would eventually be indispensable to Einstein as he ventured beyond special relativity to general relativity. Minkowski put forward his program at the beginning of an address delivered in 1908: “The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.”

Physics is about events in space and time. We locate each event in space in a reference frame equipped with a coordinate system. For example, two events are located in two spatial dimensions with the coordinate pairs x₁, y₁ and x₂, y₂ (fig. 1.5), and the spatial interval l between them is calculated by constructing a right triangle (fig. 1.6) and applying the Pythagorean theorem:

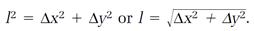
In three spatial dimensions, these equations add a term Δz² for the third dimension:

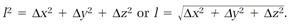 (11)

In the spirit of field theory, we treat space as a continuum and make the calculations for two neighboring events separated by the very small interval dl. That calculation follows the same recipe as equation (11), with l replaced by the much smaller dl, and Δx, Δy, Δz replaced by the smaller dx, dy, dz,

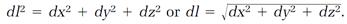 (12)

Minkowski asks us to replace this three-dimensional picture with a four dimensional one, each physical event being located by a “world point” with four coordinates, the three spatial coordinates x, y, z and the time coordinate t. How do we calculate an interval in this four-dimensional picture of space and time or better, “spacetime” comparable to dl in three dimensions? The rules of mathematical physics do not allow a simple addition of spatial and time terms, as in dt² + dx² + dy² + dz², because dx, dy, dz measure one thing (length) and dt another (time). If two terms are added in a physical equation, they must measure the same thing and have the same units.

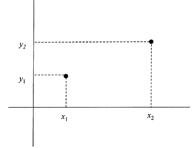
Figure 1.5. Location of two events in two spatial dimensions at the two points x₁,y₁ and x₂,y₂.

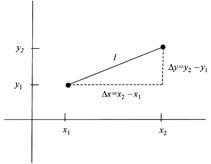
Figure 1.6. Calculation of the spatial interval l between the two events of fig.1. 5.

The simplest way to approach connections and intervals in spacetime is to imagine two events joined by that most reliable of measuring devices, a light ray. Suppose a flash of light is generated at one world point x₁, y₁, z₁, t₁, and then later detected at the world point x₂, y₂, z₂, t₂. The distance traveled by the light flash is 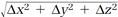 with Δx = x₂ - x₁, Δy = y₂ - y₁, and Δz = z₂ - z₁, as before. The same distance is calculated by multiplying the speed of light c by Δt, the time elapsed between the two events, that is,

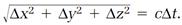
This equation is better suited to later discussions if it is rearranged slightly. Square both sides of the equation and move all terms to one side,

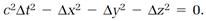
For neighboring events in the spacetime continuum, Δx, Δy, Δz, Δt become dx, dy, dz, dt, and the equation is

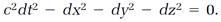 (13)

The quantity calculated is the square of a spacetime interval, and in relativity theory it is represented with ds²,

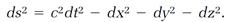 (14)

Physicists call ds a “world line element.” It is a fundamental entity in relativity theory.

However it is calculated equation (14) is only one of many possibilities the world line element ds shows how, in the four-dimensional world of spacetime, physical events are connected. For the light flash we have been discussing, ds² = 0, according to equations (13) and (14), and the events joined by ds are said to be “lightlike.” The square ds² can also be positive or negative: if positive, the events connected are “timelike,” and if negative the events are “spacelike.”

Minkowski emphasized that Einstein's world of spacetime events has a fundamental symmetry that makes the line element ds invariant in all inertial frames. If you measure ds in one frame, where the coordinates are x, y, z, t, and then ds' in another frame whose coordinates are x', y', z', t', the two measurements must be equal, ds = ds', no matter what kinds of events are connected by the line element lightlike, timelike, or spacelike. From the simple condition ds = ds', Minkowski extracted the four equations that express the relativity of the two sets of coordinates x, y, z, t and x', y', z', t'. These equations, which Lorentz had previously derived in the different context of his own theory, are now called the “Lorentz transformation.”

Einstein was not at first impressed by Minkowski's mathematical recasting of special relativity theory. He found it “banal” and called it “superfluous erudition.” But later, as he explored the mathematically more complicated world of general relativity, he found Minkowski’s concepts indispensable. He had to admit that, without Minkowski, relativity theory “might have remained stuck in its diapers.”

Physics as Geometry

Einstein's 1905 theory “in diapers” had made a powerful statement about the physical world, but Einstein knew immediately that there was room for improvement. For one thing, the theory seemed to be restricted to inertial systems. For another, it was compatible with Maxwell's electromagnetic theory, but not with another great theory inherited by Einstein, Newton's gravitation theory. To realize its potential, the theory had to recognize non-inertial systems, those accelerating relative to each other, and at the same time extend its scope to gravitation.

The first step Einstein took in this direction killed both of these birds with one stone. As he explained later, “I was sitting in a chair in the patent office at Bern when all of a sudden a thought occurred to me: ‘If a person falls freely he will not feel his own weight.’ I was startled. This simple thought made a deep impression on me. It impelled me toward a theory of gravitation.” This was Einstein's first mental image of what he would later call “the equivalence principle.” The central idea is that gravitation is relative. The person in free fall, locked inside a falling elevator, let's say, finds no evidence of gravity: everything in the elevator seems to be at rest and without weight. An outside observer, on the other hand, sees the elevator accelerating in the grip of a gravitational field.

The elevator inhabitants have the opposite experience if the elevator is removed from the gravitational field and accelerated at a constant rate upward with an attached rope (fig. 1.7). Now the outside observer sees no gravitational field, while the inside observer and all his or her belongings are held to the floor of the elevator exactly as if they were in a gravitational field. The “equivalence”

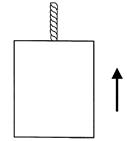
Figure 1.7. An elevator on a rope accelerated upward at a constant rate, as seen by an outside observer.

here is between an accelerating system in field-free space and an inertial system in a gravitational field. Reasoning this way, Einstein began to see how both gravitation and acceleration could be introduced into relativity theory.

The elevator-on-a-rope image (developed later by Einstein and Infeld) shows how the equivalence principle justifies an initial version of Einstein's prediction of light rays bent by gravity, which ten years later would bring the world clamoring to his door. Picture the elevator on a rope with a light ray traveling across the elevator from left to right. The outside observer sees elevator and light ray as shown in figure 1.8. Because the light ray takes a finite time to travel from wall to wall, and the elevator is accelerated upward during that time, the outside observer sees the light ray traveling the slightly curved path shown. The inside observer also sees the light ray bent, but is not aware of the acceleration and attributes the effect to the equivalent gravitational field that holds that observer to the floor of the elevator. The inside observer believes that the light ray should respond to a gravitational field because it has energy, and therefore, by the E = mc² prescription, also has mass. Like any other object with mass, the light ray responds to a gravitational field. With the equivalence principle as his guide, Einstein began in 1907 to generalize his relativity theory so that it encompassed gravity and acceleration. As he proceeded, he became increasingly convinced that he was dealing with a problem in a strange kind of geometry. Even in special relativity there are hints that acceleration and the equivalent gravitation spell violations of some of Euclid's theorems, such as the rule that the ratio of a circle's circumference to its diameter is equal to the number π. Einstein could, for example, argue from special relativity that the measured circumference-to-diameter ratio of a rapidly rotating disk had to be slightly larger than π.

By 1912, when he returned from Prague to Zurich, Einstein was hoping to find salvation in the mathematics of non-Euclidean geometry. He got some crucial help from his invaluable friend Marcel Grossmann, now professor of mathematics at the Zurich ETH, who advised him to read the work of Bernhard Riemann on differential geometry. In the 1850s, Riemann had made a general study of non- Euclidean spaces by defining the “curvature” of lines drawn in those spaces.

To calculate curvatures, Riemann used the mathematical tool that Minkowski would borrow sixty years later, the squared line element ds². As mathematicians will, Riemann imagined a completely general version of the line element equation involving any number of dimensions and including all possible quadratic terms. Consider, for example, two-dimensional Euclidean geometry with the line element

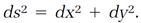 (15)

Figure 1.8. An elevator on a rope accelerated upward at a constant rate and traversed from left to right by a light ray, as seen by an outside observer.

In Riemann's scheme, we expand this to include terms in the other two mathematically possible quadratic factors, dx dy and dy dx,

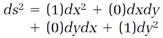
The added terms are multiplied by zero coefficients because they do not actually appear in the ds² equation; the other two terms have coefficients of one, as in equation (15). All we need to know about two-dimensional Euclidean geometry in Riemann's analysis is the four coefficients in parentheses in the last equation. We collect them in a 2 × 2 table represented by g,

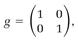
called a “metric tensor.” In three-dimensional Euclidean space the line element is

and by the same conventions the metric tensor is the 3 × 3 table

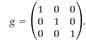
In four-dimensional Minkowski spacetime, with the line element of equation (14), the metric tensor is represented by the 4 × 4 table

The mathematical raw material for Riemann's curvature calculation is contained in the metric tensor g for the geometry in question: given a geometry defined by its metric tensor, Riemann shows how to calculate the curvature. The three metric tensors quoted happen to yield zero curvature: they specify “flat” geometries. But many other geometries have curvature and are thus non- Euclidean, as their metric tensors reveal in Riemann's analysis.

After several years of mistakes and false starts (mercifully, not part of our story), Einstein finally realized in 1915 that with Riemann's mathematical tools he could derive a field equation that intimately links gravity and geometry. His equation, reduced to its simplest form, is

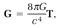 (16)

in which G is the Newtonian gravitational constant, and G and T are “tensors,” meaning that they are specially defined so that the equation has exactly the same mathematical form in all frames of reference, inertial or non-inertial. (Note that G and G have different meanings.)

The tensor G is Einstein's adaptation of Riemann's curvature calculation; it depends entirely on the relevant spacetime metric tensor g and its derivatives. The tensor T supplies all the necessary information on the gravitation source by specifying the energy and matter distribution. Thus the field equation (16) says geometry on the left side and gravity on the right. Propose a gravitation source (T) and the equation gives the Einstein tensor G, and ultimately the geometry in terms of the spacetime metric tensor g.

Gravity determines geometry in Einstein's field equations, and not surprisingly, geometry determines motion. Einstein continued with his physical argument by deriving a generalized equation of motion whose principal mathematical ingredient is the indispensable spacetime metric tensor g. Thus the sequence of the entire calculation is

Gravitation source → Curvature → Metric tensor g → Equation of motion.

The gravitation source is expressed by T, the curvature by G, the metric tensor is extracted from G, and the equation of motion is defined by g. This, in a nutshell, is one way to tell the story of Einstein's general theory of relativity. Notice that no forces are mentioned: geometry is the intermediary between gravitation and motion. The title of the story is “Physics As Geometry.”

Geometry as revealed by Einstein’s field equation (16) always means spatial curvature or non-Euclidean geometry if gravitation is present. But, except in extreme cases (for example, black holes), the extent of the curvature is extremely small. Richard Feynmann uses Einstein's theory to estimate that the Euclidean formula 4πr² for calculating the surface area of a sphere from the radius r is in error by 1.3 parts per million in the intense gravitational field at the surface of the Sun.

Einstein offered two applications of his general theory as tests of its validity. One was the calculation of the bending of light rays near the Sun, later to be confirmed in the famous Eddington and Crommelin expeditions. The other was a calculation of the orbit of Mercury, showing that the orbit is not fixed, as demanded by Newtonian theory, but slowly changes its orientation at the rate of 42.9 seconds of arc per century. This effect had been observed and measured as 43.5 seconds. When he saw this success of his theory, Einstein was euphoric. “For some days I was beyond myself with excitement,” he wrote to a friend. As Pais puts it, “From that time he knew: Nature had spoken; he had to be right.”