Karnaugh Map

In combinatorial logic minimization, a device known as a Karnaugh map is frequently used. It is similar to a truth table, but the various variables are represented along two axes and are arranged in such a way that only one input bit changes in going from one square to an adjacent square. It is also known as a Veitch diagram, K-map, or KV-map.

The Karnaugh map may be used to quickly eliminate redundant operations in a Boolean function. The easiest to read Karnaugh maps are those drawn for a function in the form of a complete product or "sum of products," where the latter name also implies the use of  and  for the AND and OR operators. In a typical truth table for such a function, the inputs are enumerated using 0 for false and 1 for true, and ordered as a counting sequence when read as positive binary integers. A truth table for a function of four variables is illustrated below.

0	0	0	0	0
0	0	0	1	0
0	0	1	0	1
0	0	1	1	1
0	1	0	0	0
0	1	0	1	0
0	1	1	0	1
0	1	1	1	1
1	0	0	0	1
1	0	0	1	0
1	0	1	0	0
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	0
1	1	1	1	0

For those rows in the table where the function value is 1 (True), a logical expression called a minterm is shown. The minterms use the overbar notation to mean NOT. When all seven minterms are accumulated,

(1)

the function is realized. This realization is not optimal, and a Karnaugh map can be used to reduce it.

A Karnaugh map for the function is shown above. It is a two dimensional layout of the truth table. Each dimension spans an adjacent, though not necessarily so, pair of variables. Instead of a counting sequence, the variables' sequence is in Gray code, so that between each pair of adjacent cells (in rows or columns) only a single variable changes state.

On the map, neighboring cells where the function value is 1 are grouped together with loops. Each loop represents minterms which can be reduced. Those variables which change within a loop can be eliminated. The validity of this, using the uppermost expression as an example, can be shown algebraically.

			(2)
			(3)
			(4)

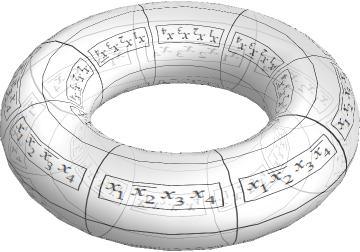
Loops can also be drawn wrapping around rows and/or columns, because the Karnaugh map (up to four variables) is really the surface of a torus.

Karnaugh maps such as in the above example can be similarly drawn for two (degenerate) or three variables. They can be employed for more than four variables (e.g., five variables by overlaying two four-variable maps), but visualization becomes a much greater chore than algebra.

There are other logic design and minimization methods based on the Karnaugh map, such as for using NAND operators instead of AND and OR.

REFERENCES

Booth, T. Digital Networks and Computer Systems. New York: Wiley, pp. 64 and 125-136, 1971.

Muroga, S. Logic Design and Switching Theory. New York: Wiley, pp. 87-90 and 281-297, 1979.