المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Complete Product |
 946
 05:01 مساءً
date: 11-1-2022 |
Author : Comtet, L 
Book or Source : Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel 
Page and Part : p. 186|
Read More
Date: 30-12-2021
1385
Date: 11-1-2022
1378
Date: 2-1-2022
1858
|
The complete products of a Boolean algebra of subsets generated by a set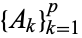 
of cardinal number 
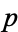are the 
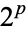Boolean functions
 |
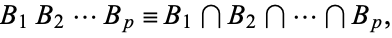(1) |
where each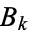 
may equal 
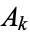or its complement 
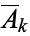. For example, the 
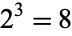complete products of 
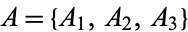are
 |
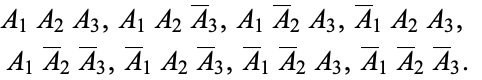(2) |
Each Boolean function has a unique representation (up to order) as a union of complete products. For example,
 |
 |
 |
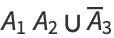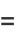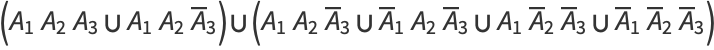(3) |
 |
 |
 |
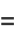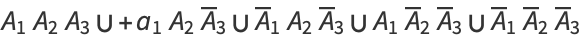(4) |
 |
 |
 |
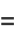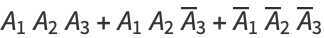(5) |
(Comtet 1974, p. 186).
REFERENCES:
Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, p. 186, 1974.
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
قسم رعاية الصحن ينهي أعماله الخاصة بإقامة الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|
