Category Product

The product of a family 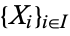 of objects of a category is an object 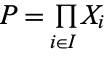, together with a family of morphisms  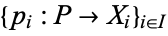such that for every object  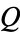and every family of morphisms  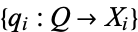there is a unique morphism  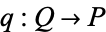such that

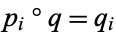for all 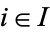. The product is unique up to isomorphisms.

In the category of sets, the product is the Cartesian product, and in the category of groups it is the group direct product. In both cases, 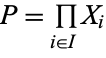, and 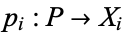 is the projection onto the 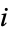th factor.

REFERENCES:

Joshi, K. D. "Products and Coproducts." Ch. 8 in Introduction to General Topology. New Delhi, India: Wiley, pp. 189-216, 1983.

Kasch, F. "Construction of Products and Coproducts." §4.80 in Modules and Rings. New York: Academic Press, pp. 80-84, 1982.

Rowen, L. "Products and Coproducts." In Ring Theory, Vol. 1. San Diego, CA: Academic Press, pp. 73-76, 1988.

Strooker, J. R. "Products and Sums." §1.5 in Introduction to Categories, Homological Algebra and Sheaf Cohomology Cambridge, England: Cambridge University Press, pp. 14-21, 1978.