


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-12-2021
Date: 14-2-2017
Date: 31-12-2021
|
A bounded lattice is an algebraic structure 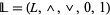 , such that
, such that 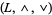 is a lattice, and the constants
is a lattice, and the constants 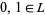 satisfy the following:
satisfy the following:
1. for all 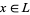 ,
, 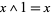 and
and 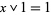 ,
,
2. for all 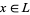 ,
, 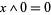 and
and 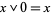 .
.
The element 1 is called the upper bound, or top of 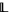 and the element 0 is called the lower bound or bottom of
and the element 0 is called the lower bound or bottom of 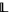 .
.
There is a natural relationship between bounded lattices and bounded lattice-ordered sets. In particular, given a bounded lattice, 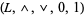 , the lattice-ordered set
, the lattice-ordered set 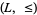 that can be defined from the lattice
that can be defined from the lattice 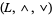 is a bounded lattice-ordered set with upper bound 1 and lower bound 0. Also, one may produce from a bounded lattice-ordered set
is a bounded lattice-ordered set with upper bound 1 and lower bound 0. Also, one may produce from a bounded lattice-ordered set 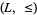 a bounded lattice
a bounded lattice 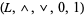 in a pedestrian manner, in essentially the same way one obtains a lattice from a lattice-ordered set. Some authors do not distinguish these structures, but here is one fundamental difference between them: A bounded lattice-ordered set
in a pedestrian manner, in essentially the same way one obtains a lattice from a lattice-ordered set. Some authors do not distinguish these structures, but here is one fundamental difference between them: A bounded lattice-ordered set 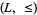 can have bounded subposets that are also lattice-ordered, but whose bounds are not the same as the bounds of
can have bounded subposets that are also lattice-ordered, but whose bounds are not the same as the bounds of 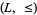 ; however, any subalgebra of a bounded lattice
; however, any subalgebra of a bounded lattice 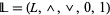 is a bounded lattice with the same upper bound and the same lower bound as the bounded lattice
is a bounded lattice with the same upper bound and the same lower bound as the bounded lattice 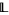 .
.
For example, let 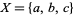 , and let
, and let 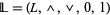 be the power set of
be the power set of 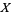 , considered as a bounded lattice:
, considered as a bounded lattice:
1. 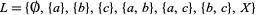
2. 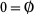 and
and 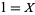
3. 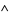 is union: for
is union: for 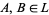 ,
, 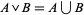
4. 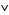 is intersection: for
is intersection: for 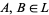 ,
, 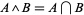 .
.
Let 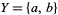 , and let
, and let 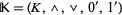 be the power set of
be the power set of 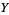 , also considered as a bounded lattice:
, also considered as a bounded lattice:
1. 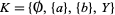
2. 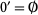 and
and 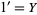
3. 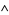 is union: for
is union: for 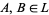 ,
, 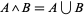
4. 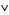 is intersection: for
is intersection: for 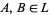 ,
, 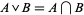 .
.
Then the lattice-ordered set 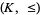 that is defined by setting
that is defined by setting 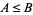 iff
iff 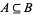 is a substructure of the lattice-ordered set
is a substructure of the lattice-ordered set 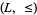 that is defined similarly on
that is defined similarly on 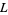 . Also, the lattice
. Also, the lattice 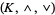 is a sublattice of the lattice
is a sublattice of the lattice 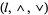 . However, the bounded lattice
. However, the bounded lattice  is not a subalgebra of the bounded lattice
is not a subalgebra of the bounded lattice 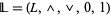 , precisely because
, precisely because 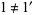 .
.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|