Laguerre's Method

A root-finding algorithm which converges to a complex root from any starting position. To motivate the formula, consider an 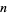th order polynomial and its derivatives,

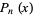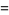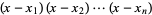			(1)
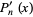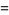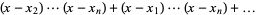			(2)
			(3)
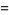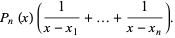			(4)

Now consider the logarithm and logarithmic derivatives of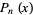 

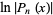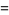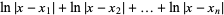			(5)
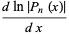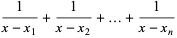			(6)
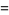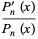			(7)
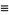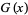			(8)
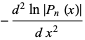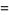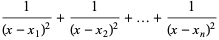			(9)
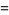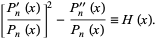			(10)

Now make "a rather drastic set of assumptions" that the root 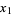 being sought is a distance  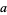from the current best guess, so

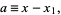(11)

while all other roots are at the same distance 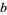, so

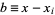(12)

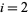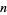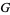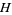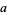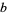for , 3, ...,  (Acton 1990; Press et al. 1992, p. 365). This allows  and  to be expressed in terms of  and  as

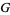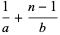			(13)
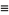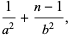			(14)

Solving these simultaneously for 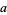 gives

(15)

where the sign is taken to give the largest magnitude for the denominator.

To apply the method, calculate 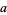 for a trial value , then use 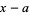 as the next trial value, and iterate until  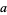becomes sufficiently small. For example, for the polynomial  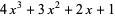with starting point 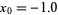, the algorithmic converges to the real root very quickly as (, , ).

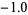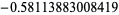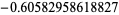Setting 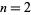 gives Halley's irrational formula.

REFERENCES:

Acton, F. S. Numerical Methods That Work, 2nd printing. Washington, DC: Math. Assoc. Amer., 1990.

Adams, D. A. "A Stopping Criterion for Polynomial Root Finding." Comm. ACM 10, 655-658, 1967.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 365-366, 1992.

Ralston, A. and Rabinowitz, P. §8.9-8.13 in A First Course in Numerical Analysis, 2nd ed. New York: McGraw-Hill, 1978.