كيف نمثل منحنى الدوال الخطية :

How do You Graph Linear Functions? 

للجواب على هذا السؤال ، نتناول بعض الدوال الخاصة البسيطة ، ونبدأ بالمثال التالي:

لكن لدينا  الدالة الخطية من الدرجة الاولى ذات الصيغة :

                                      f(x) = y = 2x + 7,

لتمثيل هذه الدالة نتبع الخطوات التالية :

اولاً : نوجد قيم للثنائية (x , y) الرئيسية في الفترة المختارة [a , b] وذلك كما يلي:

نقوم برسم المعلم المتعامد "المتجانس" ، بحيث يمكن تمثيل كل الثنائيات المدونة في الجدول، من خلال اختيار وحدة قياس مناسبة وبعده نحدد النقاط الممثلة لكل ثانية (x,y) ثم نوصل الخط بين هذه النقاط مع مراعاة الحالات الخاصة، ويتم رسم النقاط في المعلم المتعامد المتجانس(O_x , O₃ لاحظ تمثيل النقطة (x = 3 , y = 2).

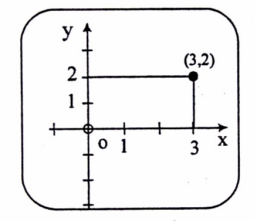
شكل (1-1)

بعد التمثيل نشير بخط ومعادلة إلى المنحنى المحصل عليه، في الحالة المدونة في المثال لدينا مستقيم ميله 2 ويقطع محور OY في النقطة (x = 0 , y = 7).

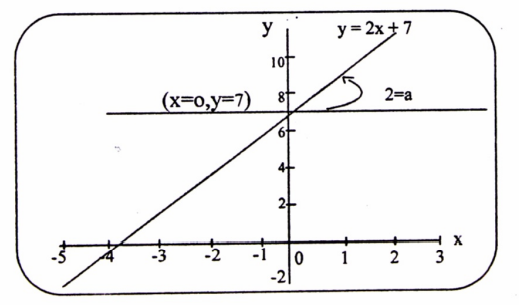
(1-2)

يمك إعادة صياغة معادلة المنحنى بخط مستقيم إذا عرفنا الميل a  ونقطة تقاطع المستقيم مع محور C = (x= 0 , y = b) ، بالمعادلة التالية:

                                      Y = f(x) = ax + b

بنفس الأسلوب يمكن حساب لميل الخط المستقيم إذا عرفنا نقطتين يمر عليهما المستقيم (x₁ , y₁) (x₂ , y₂)،  وذلك من خلال الصيغة الرياضية التالية :

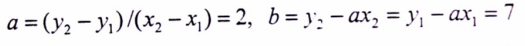
مثال (2) : أوجد تمثيل الدالة ذات المعادلة الخطية من الدرجة الأولى التالية :

                                                4x – 3y = 12      

بنفس الأسلوب السابق ، نجد النقاط الأساسية في الجدول ، ثم نمثل الثنائيات (x,y) في المعلم المتعامد  المتجانس (0_x , 0_y) . يترك الجدول للطالب . . وإليك الرسم :

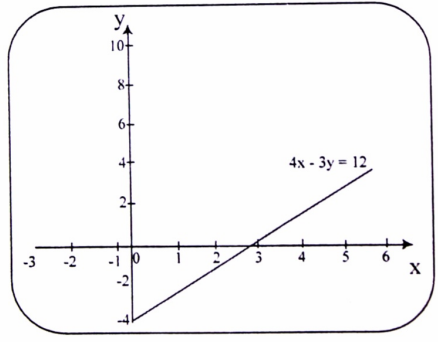
          شكل (1-3)

ملاحظة : نقول عن الدالة f إنها متزايدة (increasing) إذا كان لكل قيم d, c في المجال [a, b] حيث : ونقول عن الدالة f إنها متناقصة (decreasing) إذا كان لكل قيم d, c في المجال [a, b] حيث :

مثال (3) : مثل منحنى الدالة الخطية من الدرجة الأولى في المجال [-1 ,2] التالية :                    

                                      Y=F(x)= 2x+1

الحل :

نوجد قيم الجدول للثنائية (x,y) الرئيسية في الفترة المختارة للقيم 1- و 0 و 1 و 2

 وذلك ما يلي :

نقوم بتدوين النقاط في الجدول، ثم نمثلها في المعلم المتعامد المتجانس (O_x, O_y).

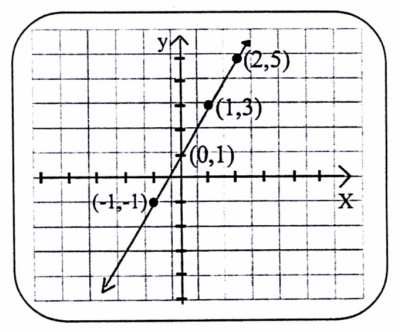
               شكل (1-4)

مثال (4) : مثل الدالة الخطية من الدرجة الاولى التالية :

                                      Y = f(x) = -0.5x + 2

الحل :

نوجد قيم الجدول للثنائية (x,y) الرئيسية في الفترة المختارة للقيم 1- و 0 و1 و 2 وذلك ما يلي:

نقوم بتدوين النقاط في الجدول، ثم نمثلها في المعمل المتعامد المتجانس (O_x , O_y).

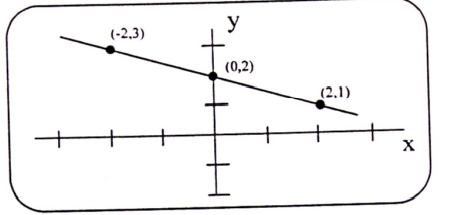
شكل (1-5)

مثال (5) : مثل الدالة الخطية الثابتة التالية :

                                      Y = f(x) = 2

الحل :

نوجد قيم الجدول للثنائية (x,y) الرئيسية في الفترة المختارة للقيم 1- و 0 و 1 و 2 وذلك ما يلي:

نقوم بتدوين النقاط في الجدول، ثم نمثلها في المعلم المتعامد المتجانس (O_x , O_y).

                             شكل (1-6)

بين ان المنحى الخاص بالدالة التكعيبية 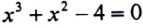 في الفترة (1,2).

مثال (6) : مثل الدالة التكعيبية التالية :

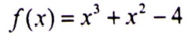
الحل : يتضح أن منحى الدالة التكعيبية f(x) = x³ + x² – 4 كما يلي:

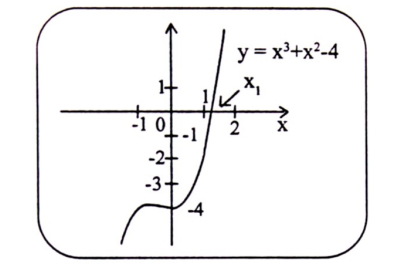
      شكل (1-7)

مثال (7) : مثل الدالة المطلقة التالية :

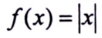
الحل :

لتوضيح الفكرة نقوم في البداية بتمثيل منحنى والذي هو كما يلي:

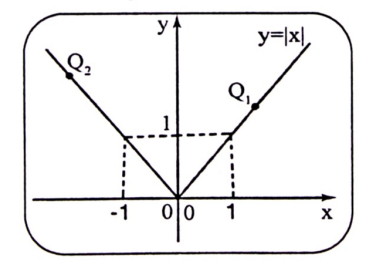
      شكل (1-8)

يتضح من التمثيل البياني أن الدالة لا تقبل مماساً عند الفاصلة x = 0 لأنه وببساطة ان قيمة نسبة التغاير عند هذه الفاصلة غير موجودة.

مثال (8) : مثل الدالة ذات القيم الصحيحة التالية :

                                                f(x) = |x|

الحل :

لتوضيح الفكرة، نقوم في البداية بتمثيل منحنى y = |x| ، ولدينا منحنى الدالة التي صيغتها هي :

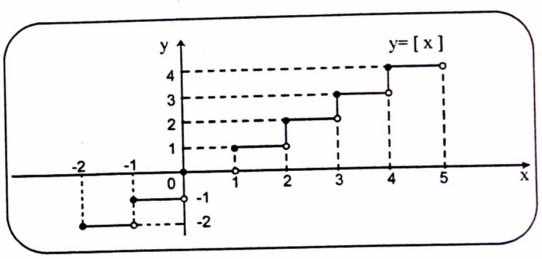
شكل (1-9)