
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-10-2021
Date: 23-8-2021
Date: 21-12-2021
|
A number of fractal curves are associated with Peano.

The Peano curve is the fractal curve illustrated above which can be written as a Lindenmayer system.
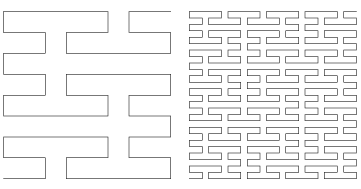
The 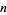 th iteration of the Peano curve illustrated above curve is implemented in the Wolfram Language as PeanoCurve[n].
th iteration of the Peano curve illustrated above curve is implemented in the Wolfram Language as PeanoCurve[n].
REFERENCES:
Dickau, R. M. "Two-Dimensional L-Systems." http://mathforum.org/advanced/robertd/lsys2d.html.
Hilbert, D. "Über die stetige Abbildung einer Linie auf ein Flachenstück." Math. Ann. 38, 459-460, 1891.
Mandelbrot, B. B. The Fractal Geometry of Nature. New York: W. H. Freeman, pp. 62-63, 1983.
Peano, G. "Sur une courbe, qui remplit une aire plane." Math. Ann. 36, 157-160, 1890.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, p. 207, 1991.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|