المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Zaslavskii Map |
 1073
 05:43 مساءً
date: 12-9-2021 |
Author : Grassberger, P. and Procaccia, I. 
Book or Source : "Measuring the Strangeness of Strange Attractors." Physica D 9 
Page and Part : ...|
Read More
Date: 6-1-2016
1406
Date: 16-2-2016
1831
Date: 9-11-2021
975
|
The two-dimensional map
 |
 |
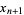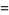![[x_n+nu(1+muy_n)+epsilonnumucos(2pix_n)] (mod 1)](https://mathworld.wolfram.com/images/equations/ZaslavskiiMap/Inline3.gif) |
(1) |
 |
 |
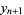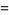![e^(-Gamma)[y_n+epsiloncos(2pix_n)],](https://mathworld.wolfram.com/images/equations/ZaslavskiiMap/Inline6.gif) |
(2) |
where
 |
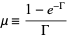(3) |
(Zaslavskii 1978). It has correlation exponent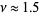 
(Grassberger and Procaccia 1983) and capacity dimension 1.39 (Russell et al. 1980).
REFERENCES:
Grassberger, P. and Procaccia, I. "Measuring the Strangeness of Strange Attractors." Physica D 9, 189-208, 1983.
Russell, D. A.; Hanson, J. D.; and Ott, E. "Dimension of Strange Attractors." Phys. Rev. Let. 45, 1175-1178, 1980.
Zaslavskii, G. M. "The Simplest Case of a Strange Attractor." Phys. Let. 69A, 145-147, 1978.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|
