المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Makeham Curve |
 1284
 02:37 صباحاً
date: 16-8-2021 |
Author : Bowers, N. L. Jr.; Gerber, H. U.; Hickman, J. C.; Jones, D. A.; and Nesbitt, C. J 
Book or Source : Actuarial Mathematics. Itasca, IL: Society of Actuaries 
Page and Part : ...|
Read More
Date: 11-2-2016
1341
Date: 23-8-2021
1302
Date: 23-12-2021
1716
|
The function defined by
 |
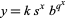which is used in actuHelvetica science for specifying a simplified mortality law (Kenney and Keeping 1962, pp. 241-242). Using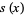 
as the probability that a newborn will achieve age 
, the Makeham law (1860) uses
 |
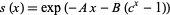for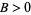 
, 
, 
, 
.
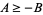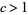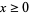REFERENCES:
Bowers, N. L. Jr.; Gerber, H. U.; Hickman, J. C.; Jones, D. A.; and Nesbitt, C. J. ActuHelvetica Mathematics. Itasca, IL: Society of Actuaries, p. 71, 1997.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, 1962.
Makeham, W. M. "On the Law of Mortality and the Construction of Annuity Tables." J. Inst. Actuaries and Assur. Mag. 8, 301-310, 1860.
Makeham, W. M. "On an Application of the Theory of the Composition of Decremental Forces." J. Inst. Actuaries and Assur. Mag. 18, 317-322, 1874.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة لجامعة سومر للمشاركة في حفل التخرج المركزي الخامس
|
|
|
