Vector Space

A vector space 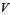 is a set that is closed under finite vector addition and scalar multiplication. The basic example is 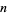-dimensional Euclidean space 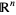, where every element is represented by a list of  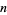real numbers, scalars are real numbers, addition is componentwise, and scalar multiplication is multiplication on each term separately.

For a general vector space, the scalars are members of a field 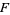, in which case  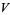is called a vector space over .

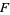Euclidean 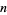-space  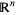is called a real vector space, and  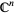is called a complex vector space.

In order for 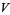 to be a vector space, the following conditions must hold for all elements  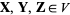and any scalars :

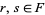1. Commutativity:

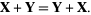(1)

2. Associativity of vector addition:

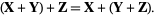(2)

3. Additive identity: For all ,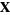

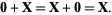(3)

4. Existence of additive inverse: For any 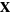, there exists a  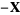such that

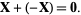(4)

5. Associativity of scalar multiplication:

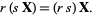(5)

6. Distributivity of scalar sums:

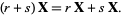(6)

7. Distributivity of vector sums:

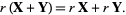(7)

8. Scalar multiplication identity:

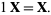(8)

Let 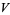 be a vector space of dimension  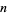over the field of  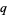elements (where  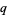is necessarily a power of a prime number). Then the number of distinct nonsingular linear operators on  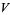is

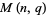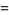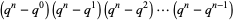			(9)
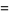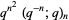			(10)

and the number of distinct 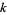-dimensional subspaces of  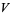is

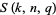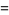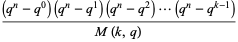			(11)
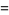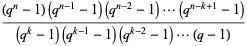			(12)
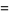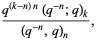			(13)

where 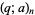 is a q-Pochhammer symbol.

A consequence of the axiom of choice is that every vector space has a vector basis.

A module is abstractly similar to a vector space, but it uses a ring to define coefficients instead of the field used for vector spaces. Modules have coefficients in much more general algebraic objects.

REFERENCES:

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 530-534, 1985.