Algebraic Unknotting Number

The algebraic unknotting number of a knot 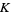 in 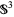 is defined as the algebraic unknotting number of the 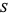-equivalence class of a Seifert matrix of 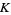. The algebraic unknotting number of an element in an 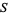-equivalent class is defined as the minimum number of algebraic unknotting operations necessary to transform the element to the 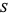-equivalence class of the zero matrix (Saeki 1999).

REFERENCES:

Fogel, M. "Knots with Algebraic Unknotting Number One." Pacific J. Math. 163, 277-295, 1994.

Murakami, H. "Algebraic Unknotting Operation, Q&A." Gen. Topology 8, 283-292, 1990.

Saeki, O. "On Algebraic Unknotting Numbers of Knots." Tokyo J. Math. 22, 425-443, 1999.