
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-5-2021
Date: 15-5-2021
Date: 1-6-2021
|
The axioms formulated by Hausdorff (1919) for his concept of a topological space. These axioms describe the properties satisfied by subsets of elements 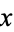 in a neighborhood set
in a neighborhood set 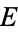 of
of 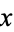 .
.
1. There corresponds to each point 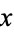 at least one neighborhood
at least one neighborhood 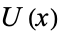 , and each neighborhood
, and each neighborhood 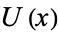 contains the point
contains the point 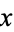 .
.
2. If 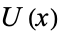 and
and 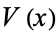 are two neighborhoods of the same point
are two neighborhoods of the same point 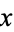 , there must exist a neighborhood
, there must exist a neighborhood 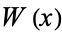 that is a subset of both.
that is a subset of both.
3. If the point 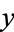 lies in
lies in 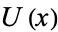 , there must exist a neighborhood
, there must exist a neighborhood 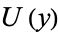 that is a subset of
that is a subset of 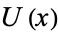 .
.
4. For two different points 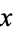 and
and 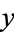 , there are two corresponding neighborhoods
, there are two corresponding neighborhoods 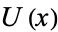 and
and 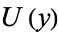 with no points in common.
with no points in common.
REFERENCES:
Hausdorff, F. Grundzüge der Mengenlehre. Leipzig, Germany: von Veit, 1914. Republished as Set Theory, 2nd ed. New York: Chelsea, 1962.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
مكتب السيد السيستاني يعزي أهالي الأحساء بوفاة العلامة الشيخ جواد الدندن
|
|
|