


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-8-2021
Date: 17-6-2021
Date: 24-6-2017
|
An orientation on an 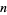 -dimensional manifold is given by a nowhere vanishing differential n-form. Alternatively, it is an bundle orientation for the tangent bundle. If an orientation exists on
-dimensional manifold is given by a nowhere vanishing differential n-form. Alternatively, it is an bundle orientation for the tangent bundle. If an orientation exists on 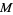 , then
, then 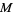 is called orientable.
is called orientable.
 |
 |
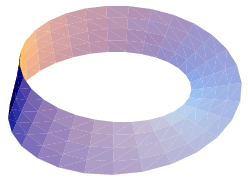
Not all manifolds are orientable, as exemplified by the Möbius strip and the Klein bottle, illustrated above.

However, an 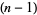 -dimensional submanifold of
-dimensional submanifold of 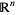 is orientable iff it has a unit normal vector field. The choice of unit determines the orientation of the submanifold. For example, the sphere
is orientable iff it has a unit normal vector field. The choice of unit determines the orientation of the submanifold. For example, the sphere 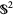 is orientable.
is orientable.
Some types of manifolds are always orientable. For instance, complex manifolds, including varieties, and also symplectic manifolds are orientable. Also, any unoriented manifold has a double cover which is oriented.
A map 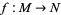 between oriented manifolds of the same dimension is called orientation preserving if the volume form on
between oriented manifolds of the same dimension is called orientation preserving if the volume form on 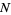 pulls back to a positive volume form on
pulls back to a positive volume form on 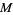 . Equivalently, the differential
. Equivalently, the differential 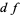 maps an oriented basis in
maps an oriented basis in 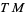 to an oriented basis in
to an oriented basis in 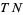 .
.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم الشؤون الفكرية ينظم ندوة ثقافية بذكرى فاجعة هدم قبور أئمة البقيع (عليهم السلام)
|
|
|