


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-7-2021
Date: 6-7-2021
Date: 3-8-2021
|
An orientable surface with one boundary component such that the boundary component of the surface is a given knot 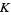 . In 1934, Seifert proved that such a surface can be constructed for any knot. The process of generating this surface is known as Seifert's algorithm. Applying Seifert's algorithm to an alternating projection of an alternating knot yields a Seifert surface of minimal knot genus.
. In 1934, Seifert proved that such a surface can be constructed for any knot. The process of generating this surface is known as Seifert's algorithm. Applying Seifert's algorithm to an alternating projection of an alternating knot yields a Seifert surface of minimal knot genus.
There are knots for which the minimal genus Seifert surface cannot be obtained by applying Seifert's algorithm to any projection of that knot, as proved by Morton in 1986 (Adams 1994, p. 105).
REFERENCES:
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 95-106, 1994.
Seifert, H. "Über das Geschlecht von Knotten." Math. Ann. 110, 571-592, 1934.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|