Jordan Curve Theorem

If 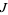 is a simple closed curve in 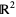, then the Jordan curve theorem, also called the Jordan-Brouwer theorem (Spanier 1966) states that  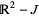has two components (an "inside" and "outside"), with  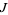the boundary of each.

The Jordan curve theorem is a standard result in algebraic topology with a rich history. A complete proof can be found in Hatcher (2002, p. 169), or in classic texts such as Spanier (1966). Recently, a proof checker was used by a Japanese-Polish team to create a "computer-checked" proof of the theorem (Grabowski 2005).

REFERENCES:

Fulton, W. Algebraic Topology: A First Course. New York: Springer-Verlag, p. 68, 1995.

Grabowski, A. "Culmination of a Complete Proof of the Jordan Curve Theorem." 2005. https://markun.cs.shinshu-u.ac.jp/mizar/jordan/jordancurve-e.html.

Hatcher, A. Algebraic Topology. Cambridge, England: Cambridge University Press, 2002. https://www.math.cornell.edu/~hatcher/AT/ATpage.html.

Knopp, K. Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, p. 14, 1996.

Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, p. 9, 1976.

Spanier, E. H. Algebraic Topology. New York: McGraw-Hill, 1966.