Five Lemma

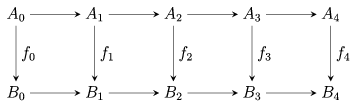
A diagram lemma which states that, given the commutative diagram of additive Abelian groups with exact rows, the following holds:

1. If  is surjective, and  and  are injective, then  is injective;

2. If  is injective, and  and  are surjective, then  is surjective.

If  and  are bijective, the hypotheses of (1) and (2) are satisfied simultaneously, and the conclusion is that  is bijective. This statement is known as the Steenrod five lemma.

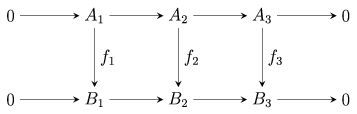
If , , , and  are the zero group, then  and  are zero maps, and thus are trivially injective and surjective. In this particular case the diagram reduces to that shown above. It follows from (1), respectively (2), that  is injective (or surjective) if  and  are. This weaker statement is sometimes referred to as the "short five lemma."

REFERENCES:

Eilenberg, S. and Steenrod, N. Foundations of Algebraic Topology. Princeton, NJ: Princeton University Press, p. 16, 1952.

Fulton, W. Algebraic Topology: A First Course. New York: Springer-Verlag, pp. 346-347, 1995.

Lang, S. Algebra, rev. 3rd ed. New York: Springer Verlag, p. 169, 2002.

Mac Lane, S. Homology. Berlin: Springer-Verlag, p. 14, 1967.

Mitchell, B. Theory of Categories. New York: Academic Press, pp. 35-36, 1965.

Munkres, J. R. Elements of Algebraic Topology. New York: Perseus Books Pub., p. 140, 1993.

Rotman, J. J. An Introduction to Algebraic Topology. New York: Springer-Verlag, pp. 98-99, 1988.

Spanier, E. H. Algebraic Topology. New York: McGraw-Hill, pp. 185-186, 1966.