


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-4-2021
Date: 29-3-2021
Date: 3-4-2021
|
The negative binomial distribution, also known as the Pascal distribution or Pólya distribution, gives the probability of 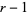 successes and
successes and  failures in
failures in 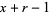 trials, and success on the
trials, and success on the 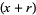 th trial. The probability density function is therefore given by
th trial. The probability density function is therefore given by
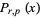 |
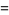 |
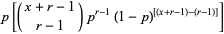 |
(1) |
 |
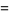 |
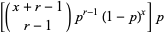 |
(2) |
 |
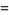 |
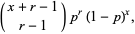 |
(3) |
where 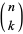 is a binomial coefficient. The distribution function is then given by
is a binomial coefficient. The distribution function is then given by
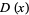 |
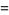 |
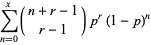 |
(4) |
 |
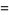 |
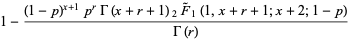 |
(5) |
 |
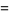 |
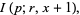 |
(6) |
where 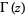 is the gamma function,
is the gamma function, 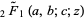 is a regularized hypergeometric function, and
is a regularized hypergeometric function, and 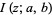 is a regularized beta function.
is a regularized beta function.
The negative binomial distribution is implemented in the Wolfram Language as NegativeBinomialDistribution[r, p].
Defining
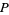 |
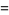 |
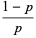 |
(7) |
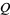 |
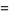 |
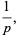 |
(8) |
the characteristic function is given by
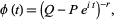 |
(9) |
and the moment-generating function by
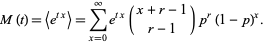 |
(10) |
Since 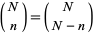 ,
,
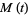 |
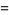 |
![p^r[1-(1-p)e^t]^(-r)](https://mathworld.wolfram.com/images/equations/NegativeBinomialDistribution/Inline36.gif) |
(11) |
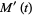 |
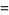 |
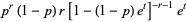 |
(12) |
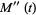 |
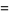 |
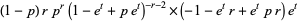 |
(13) |
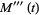 |
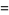 |
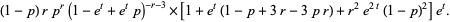 |
(14) |
The raw moments 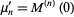 are therefore
are therefore
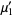 |
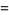 |
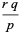 |
(15) |
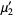 |
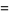 |
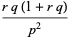 |
(16) |
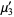 |
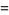 |
![(q[rp^2+3pq(r)_1+q^2(r)_2])/(p^3)](https://mathworld.wolfram.com/images/equations/NegativeBinomialDistribution/Inline55.gif) |
(17) |
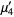 |
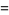 |
![(q[rp^3+7p^2q(r)_1+6pq^2(r)_2+q^3(r)_3])/(p^4),](https://mathworld.wolfram.com/images/equations/NegativeBinomialDistribution/Inline58.gif) |
(18) |
where
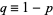 |
(19) |
and 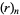 is the Pochhammer symbol. (Note that Beyer 1987, p. 487, apparently gives the mean incorrectly.)
is the Pochhammer symbol. (Note that Beyer 1987, p. 487, apparently gives the mean incorrectly.)
This gives the central moments as
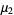 |
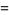 |
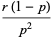 |
(20) |
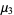 |
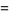 |
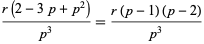 |
(21) |
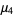 |
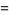 |
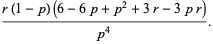 |
(22) |
The mean, variance, skewness and kurtosis excess are then
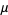 |
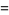 |
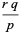 |
(23) |
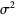 |
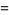 |
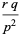 |
(24) |
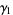 |
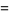 |
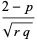 |
(25) |
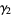 |
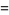 |
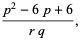 |
(26) |
which can also be written
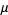 |
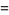 |
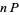 |
(27) |
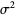 |
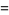 |
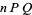 |
(28) |
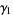 |
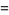 |
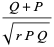 |
(29) |
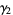 |
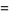 |
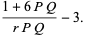 |
(30) |
The first cumulant is
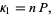 |
(31) |
and subsequent cumulants are given by the recurrence relation
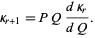 |
(32) |
REFERENCES:
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 533, 1987.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, p. 118, 1992.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
ملاكات العتبة العباسية المقدسة تُنهي أعمال غسل حرم مرقد أبي الفضل العباس (عليه السلام) وفرشه
|
|
|