
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-4-2021
Date: 6-4-2021
Date: 19-4-2021
|
Given a Poisson distribution with a rate of change 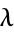 , the distribution function
, the distribution function 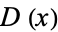 giving the waiting times until the
giving the waiting times until the 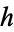 th Poisson event is
th Poisson event is
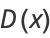 |
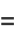 |
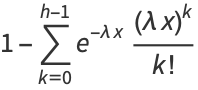 |
(1) |
 |
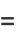 |
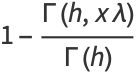 |
(2) |
for 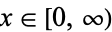 , where
, where 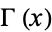 is a complete gamma function, and
is a complete gamma function, and 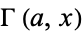 an incomplete gamma function. With
an incomplete gamma function. With 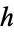 explicitly an integer, this distribution is known as the Erlang distribution, and has probability function
explicitly an integer, this distribution is known as the Erlang distribution, and has probability function
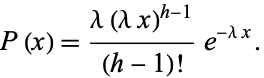 |
(3) |
It is closely related to the gamma distribution, which is obtained by letting 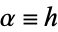 (not necessarily an integer) and defining
(not necessarily an integer) and defining 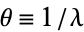 . When
. When 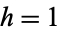 , it simplifies to the exponential distribution.
, it simplifies to the exponential distribution.
Evans et al. (2000, p. 71) write the distribution using the variables 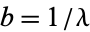 and
and 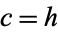 .
.
REFERENCES:
Evans, M.; Hastings, N.; and Peacock, B. "Erlang Distribution." Ch. 12 in Statistical Distributions, 3rd ed. New York: Wiley, pp. 71-73, 2000.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|