


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 31-3-2021
Date: 1-4-2021
Date: 8-3-2021
|
There are essentially three types of Fisher-Tippett extreme value distributions. The most common is the type I distribution, which are sometimes referred to as Gumbel types or just Gumbel distributions. These are distributions of an extreme order statistic for a distribution of 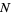 elements
elements 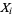 . In this work, the term "Gumbel distribution" is used to refer to the distribution corresponding to a minimum extreme value distribution (i.e., the distribution of the minimum
. In this work, the term "Gumbel distribution" is used to refer to the distribution corresponding to a minimum extreme value distribution (i.e., the distribution of the minimum 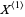 ).
).
The Gumbel distribution with location parameter 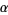 and scale parameter
and scale parameter 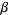 is implemented in the Wolfram Language as GumbelDistribution[alpha, beta].
is implemented in the Wolfram Language as GumbelDistribution[alpha, beta].
It has probability density function and distribution function
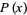 |
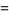 |
![1/betaexp[(x-alpha)/beta-exp((x-alpha)/beta)]](https://mathworld.wolfram.com/images/equations/GumbelDistribution/Inline8.gif) |
(1) |
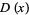 |
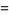 |
![1-exp[-exp((x-alpha)/beta)].](https://mathworld.wolfram.com/images/equations/GumbelDistribution/Inline11.gif) |
(2) |
The mean, variance, skewness, and kurtosis excess are
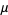 |
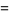 |
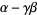 |
(3) |
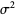 |
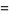 |
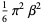 |
(4) |
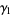 |
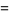 |
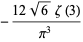 |
(5) |
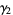 |
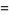 |
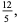 |
(6) |
where 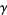 is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and 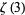 is Apéry's constant.
is Apéry's constant.
The distribution of 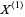 taken from a continuous uniform distribution over the unit interval has probability function
taken from a continuous uniform distribution over the unit interval has probability function
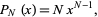 |
(7) |
and distribution function
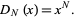 |
(8) |
The 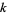 th raw moment is given by
th raw moment is given by
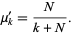 |
(9) |
The first few central moments are
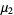 |
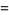 |
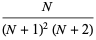 |
(10) |
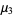 |
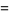 |
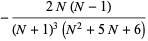 |
(11) |
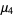 |
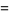 |
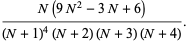 |
(12) |
The mean, variance, skewness, and kurtosis excess are therefore given by
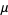 |
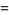 |
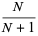 |
(13) |
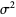 |
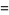 |
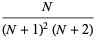 |
(14) |
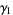 |
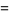 |
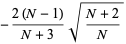 |
(15) |
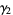 |
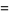 |
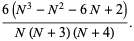 |
(16) |
If 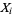 are instead taken from a standard normal distribution, then the corresponding cumulative distribution is
are instead taken from a standard normal distribution, then the corresponding cumulative distribution is
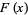 |
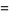 |
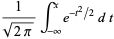 |
(17) |
 |
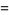 |
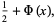 |
(18) |
where 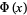 is the normal distribution function. The probability distribution of
is the normal distribution function. The probability distribution of 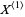 is then
is then
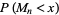 |
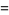 |
![[F(x)]^n](https://mathworld.wolfram.com/images/equations/GumbelDistribution/Inline60.gif) |
(19) |
 |
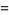 |
![n/(sqrt(2pi))int_(-infty)^x[F(t)]^(n-1)e^(-t^2/2)dt.](https://mathworld.wolfram.com/images/equations/GumbelDistribution/Inline63.gif) |
(20) |
The mean 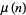 and variance
and variance 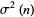 are expressible in closed form for small
are expressible in closed form for small 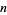 ,
,
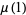 |
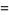 |
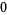 |
(21) |
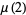 |
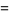 |
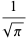 |
(22) |
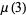 |
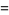 |
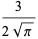 |
(23) |
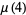 |
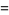 |
![3/(2sqrt(pi))[1+2/pisin^(-1)(1/3)]](https://mathworld.wolfram.com/images/equations/GumbelDistribution/Inline78.gif) |
(24) |
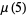 |
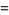 |
![5/(4sqrt(pi))[1+6/pisin^(-1)(1/3)]](https://mathworld.wolfram.com/images/equations/GumbelDistribution/Inline81.gif) |
(25) |
and
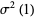 |
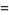 |
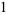 |
(26) |
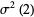 |
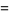 |
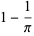 |
(27) |
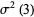 |
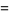 |
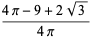 |
(28) |
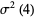 |
 |
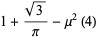 |
(29) |
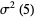 |
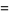 |
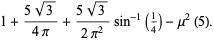 |
(30) |
No exact expression is known for 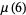 or
or 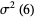 , but there is an equation connecting them
, but there is an equation connecting them
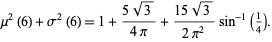 |
(31) |
REFERENCES:
Gumbel, E. J. "Multivariate Extremal Distributions." Bull. Inst. Internat. de Statistique 37, 471-475, 1960a.
Gumbel, E. J. "Distributions del valeurs extremes en plusieurs dimensions." Publ. l'Inst. de Statistique, Paris 9, 171-173, 1960b.
Gumbel, E. J. "Bivariate Logistic Distributions." J. Amer. Stat. Assoc. 56, 335-349, 1961.
Gumbel, E. J. and Mustafi, C. K. "Some Analytical Properties of Bivariate Extreme Distributions." J. Amer. Stat. Assoc. 62, 569-588, 1967.
Johnson, N.; Kotz, S.; and Balakrishnan, N. Continuous Univariate Distributions, Vol. 2, 2nd ed. New York: Wiley, 1995.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|