Mills Ratio

The Mills ratio is defined as

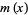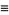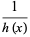			(1)
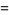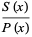			(2)
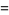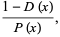			(3)

where 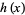 is the hazard function,  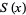is the survival function,  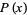is the probability density function, and  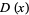is the distribution function.

For example, for the normal distribution,

(4)

which simplifies to

(5)

for the standard normal distribution. The latter function has the particularly simple continued fraction representation

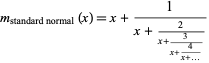(6)

(Cuyt et al. 2010, p. 376).

REFERENCES:

Boyd, A. V. "Inequalities for Mills' Ratio." Rep. Stat. Appl. Res. (Union Japan. Sci. Eng.) 6, 44-46, 1959.

Cuyt, A.; Brevik Petersen, V.; Verdonk, B.; Waadeland, H.; and Jones, W. B. Handbook of Continued Fractions for Special Functions. New York: Springer, 2010.

Evans, M.; Hastings, N.; and Peacock, B. Statistical Distributions, 3rd ed. New York: Wiley, p. 13, 2000.