المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Second-Order Eulerian Triangle |
 919
 03:25 مساءً
date: 10-1-2021 |
Author : Gessel, I. and Stanley, R. P. 
Book or Source : "Stirling Polynomials." J. Combin. Theory A 24 
Page and Part : ...|
Read More
Date: 20-1-2020
896
Date: 23-10-2019
788
Date: 7-3-2020
2620
|
 |
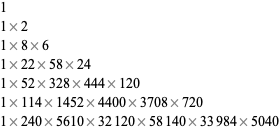(1) |
The second-order Eulerian triangle (OEIS A008517) is the number triangle defined by the recurrence
 |
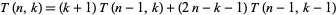(2) |
with initial conditions
 |
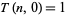(3) |
and
 |
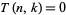(4) |
for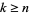 
.
REFERENCES:
Gessel, I. and Stanley, R. P. "Stirling Polynomials." J. Combin. Theory A 24, 24-33, 1978.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, p. 256, 1994.
Munch, O. J. "Om potensproduktsummer." Nordisk Matematisk Tidskrift 7, 5-19, 1959.
Sloane, N. J. A. Sequence A008517 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|
