


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-8-2020
Date: 14-9-2020
Date: 2-4-2020
|
The Pratt certificate is a primality certificate based on Fermat's little theorem converse. Prior to the work of Pratt (1975), the Lucas-Lehmer test had been regarded purely as a heuristic that worked a lot of the time (Knuth 1969). Pratt (1975) showed that Lehmer's primality heuristic could be made a nondeterministic procedure by applying it recursively to the factors of 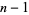 . As a consequence of this result, Pratt (1975) became the first to demonstrate that the resulting tree implies that prime factorization lies in the complexity class NP.
. As a consequence of this result, Pratt (1975) became the first to demonstrate that the resulting tree implies that prime factorization lies in the complexity class NP.
To generate a Pratt certificate, assume that 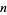 is a positive integer and
is a positive integer and 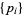 is the set of prime factors of
is the set of prime factors of 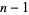 . Suppose there exists an integer
. Suppose there exists an integer  (called a "witness") such that
(called a "witness") such that 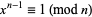 but
but 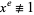 (mod
(mod 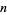 ) whenever
) whenever 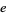 is one of
is one of 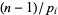 . Then Fermat's little theorem converse states that
. Then Fermat's little theorem converse states that 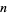 is prime (Wagon 1991, pp. 278-279).
is prime (Wagon 1991, pp. 278-279).
By applying Fermat's little theorem converse to 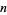 and recursively to each purported factor of
and recursively to each purported factor of 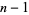 , a certificate for a given prime number can be generated. Stated another way, the Pratt certificate gives a proof that a number
, a certificate for a given prime number can be generated. Stated another way, the Pratt certificate gives a proof that a number 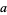 is a primitive root of the multiplicative group (mod
is a primitive root of the multiplicative group (mod 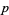 ) which, along with the fact that
) which, along with the fact that 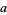 has order
has order 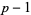 , proves that
, proves that 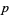 is a prime.
is a prime.
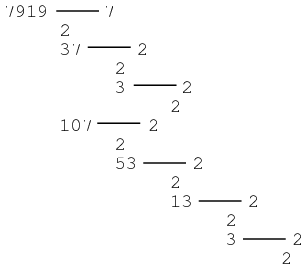
The figure above gives a certificate for the primality of 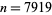 . The numbers to the right of the dashes are witnesses to the numbers to left. The set
. The numbers to the right of the dashes are witnesses to the numbers to left. The set 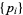 for
for 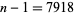 is given by
is given by 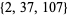 . Since
. Since 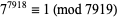 but
but 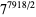 ,
, 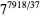 ,
, 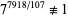 (mod 7919), 7 is a witness for 7919. The prime divisors of
(mod 7919), 7 is a witness for 7919. The prime divisors of 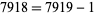 are 2, 37, and 107. 2 is a so-called "self-witness" (i.e., it is recognized as a prime without further ado), and the remainder of the witnesses are shown as a nested tree. Together, they certify that 7919 is indeed prime. Because it requires the factorization of
are 2, 37, and 107. 2 is a so-called "self-witness" (i.e., it is recognized as a prime without further ado), and the remainder of the witnesses are shown as a nested tree. Together, they certify that 7919 is indeed prime. Because it requires the factorization of 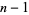 , the method of Pratt certificates is best applied to small numbers (or those numbers
, the method of Pratt certificates is best applied to small numbers (or those numbers 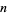 known to have easily factorable
known to have easily factorable 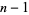 ).
).
A Pratt certificate is quicker to generate for small numbers than are other types of primality certificates. The Wolfram Language function ProvablePrimeQ[n] in the Wolfram Language package PrimalityProving` therefore generates an Atkin-Goldwasser-Kilian-Morain certificate only for numbers above a certain limit (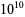 by default), and a Pratt certificate for smaller numbers.
by default), and a Pratt certificate for smaller numbers.
REFERENCES:
Knuth, D. E. §4.5.4 in The Art of Computer Programming, Vol. 2: Seminumerical Algorithms. Reading, MA: Addison-Wesley, 1969.
Pratt, V. "Every Prime Has a Succinct Certificate." SIAM J. Comput. 4, 214-220, 1975.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 278-285, 1991.
Wilf, H. §4.10 in Algorithms and Complexity. Englewood Cliffs, NJ: Prentice-Hall, 1986.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|