


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-11-2020
Date: 30-1-2021
Date: 22-8-2020
|
There are two definitions of the supersingular primes: one group-theoretic, and the other number-theoretic.
Group-theoretically, let 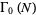 be the modular group Gamma0, and let
be the modular group Gamma0, and let 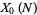 be the compactification (by adding cusps) of
be the compactification (by adding cusps) of 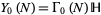 , where
, where 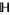 is the upper half-plane. Also define
is the upper half-plane. Also define 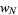 to be the Fricke involution defined by the block matrix
to be the Fricke involution defined by the block matrix ![[[0,-1],[N,0]]](https://mathworld.wolfram.com/images/equations/SupersingularPrime/Inline6.gif) . For
. For 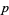 a prime, define
a prime, define 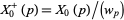 . Then
. Then 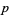 is a supersingular prime if the genus of
is a supersingular prime if the genus of 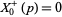 .
.
The number-theoretic definition involves supersingular elliptic curves defined over the algebraic closure of the finite field 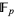 . They have their j-invariant in
. They have their j-invariant in 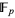 .
.
Supersingular curves were mentioned by Charlie the math genius in the Season 2 episode "In Plain Sight" of the television crime drama NUMB3RS.
There are exactly 15 supersingular primes: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 47, 59, and 71 (OEIS A002267). The supersingular primes are exactly the set of primes that divide the group order of the Monster group.
REFERENCES:
Conway, J. H.; Curtis, R. T.; Norton, S. P.; Parker, R. A.; and Wilson, R. A. Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups. Oxford, England: Clarendon Press, 1985.
Conway, J. H. and Norton, S. P. "Monstrous Moonshine." Bull. London Math. Soc. 11, 308-339, 1979.
Ogg, A. P. "Modular Functions." In The Santa Cruz Conference on Finite Groups. Held at the University of California, Santa Cruz, Calif., June 25-July 20, 1979 (Ed. B. Cooperstein and G. Mason). Providence, RI: Amer. Math. Soc., pp. 521-532, 1980.
Silverman, J. H. The Arithmetic of Elliptic Curves. New York: Springer-Verlag, 1986.
Silverman, J. H. The Arithmetic of Elliptic Curves II. New York: Springer-Verlag, 1994.
Sloane, N. J. A. Sequence A002267 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|