


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-11-2019
Date: 13-1-2021
Date: 21-9-2020
|
Lehmer's totient problem asks if there exist any composite numbers 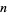 such that
such that 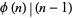 , where
, where 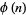 is the totient function? No such numbers are known. However, any such an
is the totient function? No such numbers are known. However, any such an 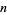 would need to be a Carmichael number, since for every element
would need to be a Carmichael number, since for every element 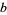 in the integers (mod
in the integers (mod 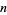 ),
), 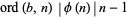 , so
, so 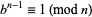 and
and 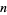 is a Carmichael number.
is a Carmichael number.
In 1932, Lehmer showed that such an 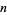 must be odd and squarefree, and that the number of distinct prime factors
must be odd and squarefree, and that the number of distinct prime factors 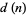 must satisfy
must satisfy 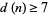 . This was subsequently extended to
. This was subsequently extended to 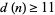 . The best current result is
. The best current result is 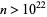 and
and 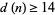 , improving the
, improving the 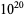 lower bound of Cohen and Hagis (1980) since there are no Carmichael numbers less than
lower bound of Cohen and Hagis (1980) since there are no Carmichael numbers less than 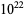 having
having 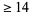 distinct prime factors; Pinch). However, even better results are known in the special cases
distinct prime factors; Pinch). However, even better results are known in the special cases 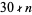 , in which case
, in which case 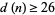 (Wall 1980), and
(Wall 1980), and 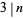 , in which case
, in which case 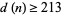 and
and 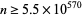 (Lieuwens 1970).
(Lieuwens 1970).
REFERENCES:
Cohen, G. L. and Hagis, P. Jr. "On the Number of Prime Factors of 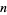 is
is 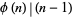 ." Nieuw Arch. Wisk. 28, 177-185, 1980.
." Nieuw Arch. Wisk. 28, 177-185, 1980.
Cohen, G. L. and Segal, S. L. "A Note Concerning Those 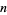 for which
for which 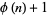 Divides
Divides 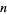 ." Fib. Quart. 27, 285-286, 1989.
." Fib. Quart. 27, 285-286, 1989.
Lieuwens, E. "Do There Exist Composite Numbers for Which 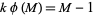 Holds?" Nieuw Arch. Wisk. 18, 165-169, 1970.
Holds?" Nieuw Arch. Wisk. 18, 165-169, 1970.
Pinch, R. G. E. ftp://ftp.dpmms.cam.ac.uk/pub/Carmichael/table.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 27-28, 1989.
Wall, D. W. "Conditions for 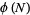 to Properly Divide
to Properly Divide 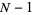 ." In A Collection of Manuscripts Related to the Fibonacci Sequence (Ed. V. E. Hoggatt and M. V. E. Bicknell-Johnson). San Jose, CA: Fibonacci Assoc., pp. 205-208, 1980.
." In A Collection of Manuscripts Related to the Fibonacci Sequence (Ed. V. E. Hoggatt and M. V. E. Bicknell-Johnson). San Jose, CA: Fibonacci Assoc., pp. 205-208, 1980.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|