
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-10-2020
Date: 31-1-2020
Date: 17-10-2019
|
For 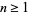 , let
, let 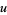 and
and 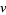 be integers with
be integers with 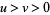 such that the Euclidean algorithm applied to
such that the Euclidean algorithm applied to 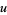 and
and 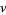 requires exactly
requires exactly 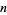 division steps and such that
division steps and such that 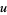 is as small as possible satisfying these conditions. Then
is as small as possible satisfying these conditions. Then 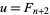 and
and 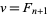 , where
, where 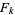 is a Fibonacci number (Knuth 1998, p. 343).
is a Fibonacci number (Knuth 1998, p. 343).
Furthermore, the number of steps in the Euclidean algorithm never exceeds 5 times the number of digits in the smaller number. In fact, the bound 5 can be further reduced to 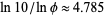 , where
, where 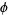 is the golden ratio.
is the golden ratio.
REFERENCES:
Honsberger, R. "A Theorem of Gabriel Lamé." Ch. 7 in Mathematical Gems II. Washington, DC: Math. Assoc. Amer., pp. 54-57, 1976.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1998.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|