


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-12-2020
Date: 16-8-2020
Date: 9-8-2020
|
The weak law of large numbers (cf. the strong law of large numbers) is a result in probability theory also known as Bernoulli's theorem. Let 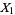 , ...,
, ..., 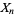 be a sequence of independent and identically distributed random variables, each having a mean
be a sequence of independent and identically distributed random variables, each having a mean 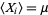 and standard deviation
and standard deviation 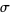 . Define a new variable
. Define a new variable
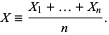 |
(1) |
Then, as 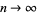 , the sample mean
, the sample mean 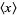 equals the population mean
equals the population mean 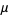 of each variable.
of each variable.
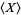 |
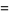 |
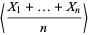 |
(2) |
 |
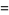 |
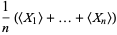 |
(3) |
 |
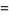 |
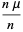 |
(4) |
 |
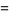 |
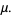 |
(5) |
In addition,
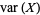 |
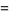 |
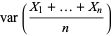 |
(6) |
 |
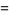 |
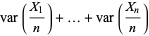 |
(7) |
 |
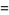 |
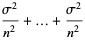 |
(8) |
 |
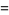 |
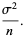 |
(9) |
Therefore, by the Chebyshev inequality, for all 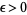 ,
,
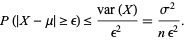 |
(10) |
As 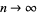 , it then follows that
, it then follows that
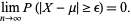 |
(11) |
(Khinchin 1929). Stated another way, the probability that the average 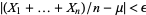 for
for 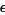 an arbitrary positive quantity approaches 1 as
an arbitrary positive quantity approaches 1 as 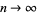 (Feller 1968, pp. 228-229).
(Feller 1968, pp. 228-229).
REFERENCES:
Feller, W. "Laws of Large Numbers." Ch. 10 in An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, pp. 228-247, 1968.
Feller, W. "Law of Large Numbers for Identically Distributed Variables." §7.7 in An Introduction to Probability Theory and Its Applications, Vol. 2, 3rd ed. New York: Wiley, pp. 231-234, 1971.
Khinchin, A. "Sur la loi des grands nombres." Comptes rendus de l'Académie des Sciences 189, 477-479, 1929.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 69-71, 1984.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|