Bartlett Function

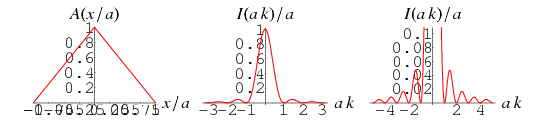
The apodization function

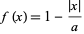(1)

which is a generalization of the one-argument triangle function. Its full width at half maximum is .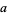

It has instrument function

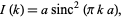(2)

where 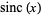 is the sinc function. The peak of  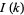is 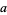, and the full width at half maximum is given by setting  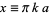and numerically solving

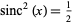(3)

for 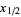, yielding

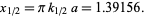(4)

Therefore, with ,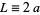

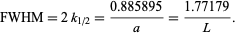(5)

The function 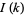 is always positive, so there are no negative sidelobes. The extrema are given by differentiating  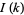with respect to 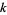, defining 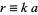, and setting equal to 0,

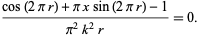(6)

Solving this numerically gives minima of 0 at 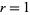, 2, 3, ..., and sidelobes of 0.047190, 0.01648, 0.00834029, ... at 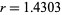, 2.45892, 3.47089, ....

REFERENCES:

Bartlett, M. S. "Periodogram Analysis and Continuous Spectra." Biometrika 37, 1-16, 1950.

Blackman, R. B. and Tukey, J. W. The Measurement of Power Spectra, From the Point of View of Communications Engineering. New York: Dover, pp. 98-99, 1959.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 554-556, 1992.