Multiplicative Order

Let 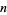 be a positive number having primitive roots. If  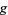is a primitive root of 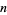, then the numbers 1, 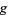, , 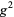...,  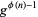form a reduced residue system modulo 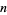, where  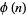is the totient function. In this set, there are  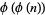primitive roots, and these are the numbers 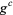, where  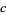is relatively prime to .

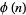The smallest exponent 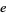 for which 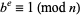, where  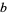and 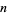 are given numbers, is called the multiplicative order (or sometimes haupt-exponent or modulo order) of  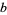(mod ).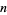

The multiplicative order is implemented in the Wolfram Language as MultiplicativeOrder[g, n].

The number of bases having multiplicative order 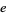 is 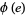, where  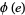is the totient function. Cunningham (1922) published the multiplicative order for primes to 25409 and bases 2, 3, 5, 6, 7, 10, 11, and 12.

Multiplicative orders exist for 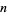 that are relatively prime to 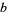. For example, the multiplicative order of 10 (mod 7) is 6, since

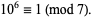(1)

The multiplicative order of 10 mod an integer  relatively prime to 10 gives the period of the decimal expansion of the reciprocal of  (Glaisher 1878, Lehmer 1941). For example, the haupt-exponent of 10 (mod 13) is 6, and

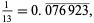(2)

which has period 6.

The following table gives the first few multiplicative orders for bases 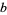 (mod 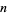), where  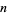is the series of numbers relatively prime to .

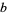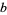	OEIS	haupt-exponents
2	A002326	2, 4, 3, 6, 10, 12, 4, 8, 18, 6, 11, 20, 18, ...
3	A050975	1, 2, 4, 6, 2, 4, 5, 3, 6, 4, 16, 18, 4, 5, ...
4	A050976	1, 2, 3, 3, 5, 6, 2, 4, 9, 3, 11, 10, 9, 14, ...
5	A050977	1, 2, 1, 2, 6, 2, 6, 5, 2, 4, 6, 4, 16, 6, 9, ...
6	A050978	1, 2, 10, 12, 16, 9, 11, 5, 14, ...
7	A050979	1, 1, 2, 4, 1, 2, 3, 4, 10, 2, 12, 4, 2, 16, ...
8	A050980	2, 4, 1, 2, 10, 4, 4, 8, 6, 2, 11, 20, 6, 28, ...
9	A050981	1, 1, 2, 3, 1, 2, 5, 3, 3, 2, 8, 9, 2, 5, 11, ...
10	A002329	1, 6, 1, 2, 6, 16, 18, 6, 22, 3, 28, ...

If 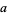 is an arbitrary integer relatively prime to 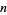, then there exists among the numbers 0, 1, 2, ...,  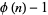exactly one number  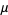such that

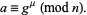(3)

The number 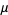 is then called the generalized multiplicative order (or discrete logarithm; Schneier 1996, p. 501) of  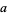with respect to the base  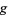modulo 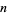. Note that Nagell (1951, p. 112) instead uses the term "index" and writes

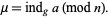(4)

For example, the number 7 is the least positive primitive root of 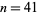, and since 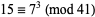, the number 15 has multiplicative order 3 with respect to base 7 (modulo 41) (Nagell 1951, p. 112).

The generalized multiplicative order is implemented in the Wolfram Language as MultiplicativeOrder[g, n, 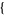a1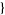], or more generally as MultiplicativeOrder[g, n, 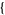a1, a2, ...].

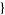If the primitive roots 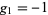 and 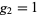 are chosen, the resulting function is called the suborder function and is denoted 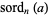. If the single primitive root  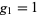is chosen, then the function reduces to "the" (i.e., ungeneralized) multiplicative order, denoted 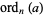, implemented in the Wolfram Language as MultiplicativeOrder[a, n]. This function is sometimes also known as the discrete logarithm (or, more confusingly, as the "index," a term that Nagell applied to the case of general ).

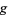REFERENCES:

Burton, D. M. "The Order of an Integer Modulo 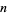." §8.1 in Elementary Number Theory, 4th ed. Dubuque, IA: William C. Brown Publishers, pp. 184-190, 1989.

Cunningham, A. Haupt-Exponents, Residue Indices, Primitive Roots. London: F. Hodgson, 1922.

Glaisher, J. W. L. "Periods of Reciprocals of Integers Prime to 10." Proc. Cambridge Philos. Soc. 3, 185-206, 1878.

Lehmer, D. H. "Guide to Tables in the Theory of Numbers." Bulletin No. 105. Washington, DC: National Research Council, pp. 7-12, 1941.

Nagell, T. "Exponent of an Integer Modulo 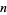" and "The Index Calculus." §31 and 33 in Introduction to Number Theory. New York: Wiley, pp. 102-106 and 111-115, 1951.

Odlyzko, A. "Discrete Logarithms: The Past and the Future." http://www.dtc.umn.edu/~odlyzko/doc/discrete.logs.future.pdf.

Schneier, B Applied Cryptography: Protocols, Algorithms, and Source Code in C, 2nd ed. New York: Wiley, 1996.

Sloane, N. J. A. Sequences A002326/M0936, A002329/M4045, A050975, A050976, A050977, A050978, A050979, A050980, and A050981 in "The On-Line Encyclopedia of Integer Sequences."